ဤ Tutorial သည် Binary Search & Java ရှိ Recursive Binary Search သည် ၎င်း၏ Algorithm၊ အကောင်အထည်ဖော်ခြင်းနှင့် Java Binary Seach Code နမူနာများနှင့်အတူ-
Java ရှိ ဒွိရှာဖွေမှုတစ်ခုသည် စုစည်းမှုတစ်ခုအတွင်းရှိ ပစ်မှတ်တန်ဖိုး သို့မဟုတ် သော့ကိုရှာဖွေရန်အတွက် အသုံးပြုသည့်နည်းပညာတစ်ခုဖြစ်သည်။ ၎င်းသည် သော့တစ်ခုကိုရှာဖွေရန် “divide and conquer” နည်းပညာကို အသုံးပြုသည့် နည်းပညာတစ်ခုဖြစ်သည်။
သော့ကိုရှာဖွေရန်အတွက် Binary search ကိုအသုံးပြုမည့် စုစည်းမှုကို ငယ်စဉ်လိုက် စီရန် လိုအပ်ပါသည်။
ပုံမှန်အားဖြင့်၊ ပရိုဂရမ်းမင်းဘာသာစကားအများစုသည် Linear ရှာဖွေမှု၊ Binary ရှာဖွေမှုနှင့် စုဆောင်းမှုတွင်ဒေတာရှာဖွေရန်အသုံးပြုသည့် Hashing နည်းပညာများကို ပံ့ပိုးပေးသည်။ ကျွန်ုပ်တို့၏ နောက်ဆက်တွဲသင်ခန်းစာများတွင် hashing ကို လေ့လာပါမည်။

Binary Search In Java
Linear search သည် အခြေခံနည်းပညာတစ်ခုဖြစ်သည်။ ဤနည်းစနစ်တွင်၊ array သည် ဆင့်ကဲဖြတ်သွားမည်ဖြစ်ပြီး သော့ကိုတွေ့သည် သို့မဟုတ် array ၏အဆုံးသို့မရောက်မချင်း ဒြပ်စင်တစ်ခုစီကို သော့နှင့်နှိုင်းယှဉ်ပါသည်။
Linear ရှာဖွေမှုကို လက်တွေ့အသုံးချမှုတွင် ရှားရှားပါးပါးအသုံးပြုပါသည်။ Binary Search သည် linear ရှာဖွေမှုထက် များစွာပိုမိုမြန်ဆန်သောကြောင့် အသုံးအများဆုံးနည်းပညာဖြစ်သည်။
Java သည် binary ရှာဖွေမှုလုပ်ဆောင်ရန် နည်းလမ်းသုံးသွယ်ကို ပံ့ပိုးပေးသည်-
- အသုံးပြုခြင်း ထပ်ခါထပ်ခါ ချဉ်းကပ်မှု
- ပြန်ယူနည်းကို အသုံးပြုခြင်း
- Arrays.binarySearch () နည်းလမ်းကို အသုံးပြုခြင်း။
ဤသင်ခန်းစာတွင်၊ ဤအရာအားလုံးကို အကောင်အထည်ဖော်ပြီး ဆွေးနွေးပါမည်။ နည်းလမ်း 3 ခု။
Java တွင် Binary Search အတွက် Algorithm
ဒွိစုံရှာဖွေမှုနည်းလမ်း၊ စုစည်းမှုကို တစ်ဝက်သို့ ထပ်ခါတလဲလဲ ပိုင်းခြားထားပြီး သော့သည် စုစည်းမှု၏ အလယ်ဒြပ်ထက် နည်းသည် သို့မဟုတ် ပိုကြီးသည်ပေါ်မူတည်၍ အဓိကဒြပ်စင်အား စုစည်းမှု၏ ဘယ် သို့မဟုတ် ညာဘက်တစ်ဝက်တွင် ရှာဖွေမည်ဖြစ်သည်။
ရိုးရှင်းသော Binary Search Algorithm သည် အောက်ပါအတိုင်းဖြစ်သည်-
- စုစည်းမှု၏ အလယ်ဒြပ်စင်ကို တွက်ချက်ပါ။
- အဓိကအရာများကို အလယ်ဒြပ်စင်နှင့် နှိုင်းယှဉ်ပါ။
- သော့ = အလယ်ဒြပ်စင်ဖြစ်ပါက၊ တွေ့ရှိသောကီးအတွက် အလယ်အညွှန်းအနေအထားကို ကျွန်ုပ်တို့ ပြန်ပေးပါသည်။
- အခြားသော့ဆိုလျှင် > အလယ်ဒြပ်စင်၊ ထို့နောက် သော့သည် စုစည်းမှု၏ ညာဘက်ခြမ်းတွင် ရှိသည်။ ထို့ကြောင့် စုစည်းမှု၏ အောက် (ညာဘက်) တစ်ဝက်ရှိ အဆင့် 1 မှ 3 ကို ပြန်လုပ်ပါ။
- အခြားသော့ အလယ်ဒြပ်စင်၊ ထို့နောက် သော့သည် စုစည်းမှု၏ အပေါ်ပိုင်းတစ်ဝက်တွင် ရှိသည်။ ထို့ကြောင့် သင်သည် အထက်တစ်ဝက်တွင် binary ရှာဖွေမှုကို ထပ်လုပ်ရန် လိုအပ်သည်။
အထက်အဆင့်များမှ သင်တွေ့မြင်ရသည့်အတိုင်း Binary ရှာဖွေမှုတွင်၊ ပထမအကြိမ်နှိုင်းယှဉ်ပြီးနောက် စုစည်းမှုတစ်ဝက်ကို လျစ်လျူရှုထားသည်။
တူညီသောအဆင့်များကို ထပ်ခါတလဲလဲရှာဖွေခြင်းနှင့် ထပ်ခါတလဲလဲ ဒွိစုံရှာဖွေခြင်းများ ပြုလုပ်နိုင်သည်ကို သတိပြုပါ။
ဥပမာတစ်ခုအသုံးပြု၍ binary ရှာဖွေမှု algorithm ကို သရုပ်ဖော်ကြည့်ကြပါစို့။
ဥပမာ၊ အောက်ပါ အစိတ်အပိုင်း 10 ခုမှ စီထားသော array ကို ယူပါ။

array ၏ အလယ်တည်နေရာကို တွက်ကြည့်ရအောင်။
Mid = 0+9/2 = 4
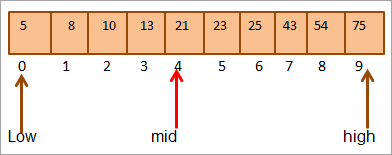
#1) Key = 21
ပထမ၊ ကျွန်ုပ်တို့သည် သော့တန်ဖိုးနှင့် နှိုင်းယှဉ်မည် [mid] element နဲ့ element value at ဆိုတာကို တွေ့ပါတယ်။mid = 21.
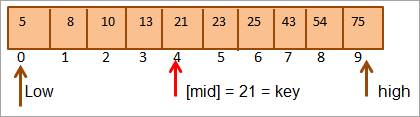
ထို့ကြောင့် ထိုသော့ = [mid] ကို ရှာတွေ့သည်။ ထို့ကြောင့် သော့ကို array တွင် position 4 တွင်တွေ့နိုင်သည်။
#2) Key = 25
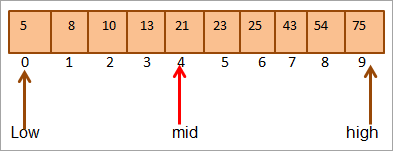
သော့ကို ဦးစွာနှိုင်းယှဉ်ပါသည်။ အလယ်အလတ်မှတန်ဖိုး။ (21 25) အနေဖြင့် array ၏အပေါ်ပိုင်းတစ်ဝက်ရှိ သော့ကိုကျွန်ုပ်တို့တိုက်ရိုက်ရှာဖွေပါမည်။
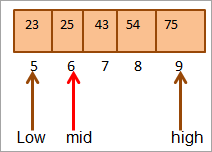
ယခုတစ်ဖန် အထက်ပိုင်းတစ်ဝက်အတွက် အလယ်ကိုရှာပါမည်။ array။
Mid = 4+9/2 = 6
တည်နေရာ [mid] = 25
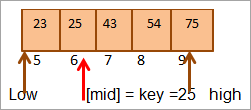
ယခု ကျွန်ုပ်တို့ အဓိကဒြပ်စင်ကို အလယ်ဒြပ်စင်နှင့် နှိုင်းယှဉ်ပါ။ ထို့ကြောင့် (25 == 25) ထို့ကြောင့် တည်နေရာ [mid] = 6 တွင် သော့ကိုကျွန်ုပ်တို့တွေ့ရှိခဲ့ပါသည်။
ထို့ကြောင့် array ကို ထပ်ခါတလဲလဲခွဲဝေပြီး အဓိကဒြပ်စင်ကို အလယ်နှင့် နှိုင်းယှဉ်ခြင်းဖြင့်၊ တစ်ဝက်ကို မည်သည့်အတွက်ကြောင့်ဖြစ်သည်ကို ဆုံးဖြတ်ပါသည်။ သော့ကိုရှာပါ။ Binary Search သည် အချိန်နှင့် မှန်ကန်မှုတွင် ပိုမိုထိရောက်ပြီး အလွန်မြန်ဆန်ပါသည်။
Binary Search Implementation Java
အထက်ပါ algorithm ကိုအသုံးပြု၍ Java တွင် Binary ရှာဖွေမှုပရိုဂရမ်တစ်ခုကို အသုံးပြုကြပါစို့။ ထပ်ခါတလဲလဲ ရေးပါတယ်။ ဤပရိုဂရမ်တွင်၊ ကျွန်ုပ်တို့သည် နမူနာ array တစ်ခုကိုယူပြီး ဤ array တွင် binary ရှာဖွေမှုကို လုပ်ဆောင်ပါသည်။
import java.util.*; class Main{ public static void main(String args[]){ int numArray[] = {5,10,15,20,25,30,35}; System.out.println("The input array: " + Arrays.toString(numArray)); //key to be searched int key = 20; System.out.println("\nKey to be searched=" + key); //set first to first index int first = 0; //set last to last elements in array int last=numArray.length-1; //calculate mid of the array int mid = (first + last)/2; //while first and last do not overlap while( first = last ){ //if the mid key, then key to be searched is in the first half of array if ( numArray[mid] last ){ System.out.println("Element is not found!"); } } } Output-
Input array- [5၊ 10၊ 15၊ 20 ၊ 25၊ 30၊ 35]
ရှာဖွေရမည့်သော့=20
ဒြပ်စင်ကို အညွှန်းတွင်တွေ့ရသည်- 3
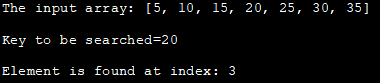
အထက်ပါပရိုဂရမ် Binary ရှာဖွေမှု၏ ထပ်ခါထပ်ခါ ချဉ်းကပ်မှုကို ပြသသည်။ အစပိုင်းတွင်၊ array တစ်ခုအား ကြေညာပြီး၊ ထို့နောက် ရှာဖွေရမည့်သော့ကို သတ်မှတ်သည်။
အခင်းအကျင်း၏အလယ်ကို တွက်ချက်ပြီးနောက်၊ သော့ကို အလယ်ဒြပ်စင်နှင့် နှိုင်းယှဉ်သည်။ အဲဒီအခါမှာ ရှိမရှိပေါ် မူတည်ပါတယ်။သော့သည် သော့ထက်နည်းသည် သို့မဟုတ် ပိုကြီးသည်၊ သော့ကို array ၏ အောက် သို့မဟုတ် အထက်တစ်ဝက်တွင် အသီးသီးရှာဖွေသည်။
Recursive Binary Search တွင် Java
သင်သည် binary ရှာဖွေမှုကိုလည်း လုပ်ဆောင်နိုင်သည်။ recursion နည်းပညာကို အသုံးပြု. ဤနေရာတွင်၊ သော့ကိုမတွေ့မချင်း သို့မဟုတ် စာရင်းတစ်ခုလုံးကုန်သွားသည်အထိ ဒွိစုံရှာဖွေမှုနည်းလမ်းကို ထပ်ခါတလဲလဲခေါ်ဆိုပါသည်။
ပြန်ကောက်ထားသော binary ရှာဖွေမှုကို အကောင်အထည်ဖော်သည့်ပရိုဂရမ်ကို အောက်တွင်ဖော်ပြထားသည်-
import java.util.*; class Main{ //recursive method for binary search public static int binary_Search(int intArray[], int low, int high, int key){ //if array is in order then perform binary search on the array if (high>=low){ //calculate mid int mid = low + (high - low)/2; //if key =intArray[mid] return mid if (intArray[mid] == key){ return mid; } //if intArray[mid] > key then key is in left half of array if (intArray[mid] > key){ return binary_Search(intArray, low, mid-1, key);//recursively search for key }else //key is in right half of the array { return binary_Search(intArray, mid+1, high, key);//recursively search for key } } return -1; } public static void main(String args[]){ //define array and key int intArray[] = {1,11,21,31,41,51,61,71,81,91}; System.out.println("Input List: " + Arrays.toString(intArray)); int key = 31; System.out.println("\nThe key to be searched:" + key); int high=intArray.length-1; //call binary search method int result = binary_Search(intArray,0,high,key); //print the result if (result == -1) System.out.println("\nKey not found in given list!"); else System.out.println("\nKey is found at location: "+result + " in the list"); } } အထွက်-
ထည့်သွင်းမှုစာရင်း- [1၊ 11၊ 21၊ 31၊ 41၊ 51၊ 61၊ 71၊ 81၊ 91
ရှာဖွေရမည့်သော့ :
သော့ကို တည်နေရာတွင် တွေ့ရသည်- စာရင်းထဲတွင် 3 ခု
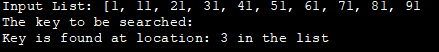
Arrays.binarySearch () နည်းလမ်းကို အသုံးပြုခြင်း။
Java ရှိ Arrays အတန်းသည် ပေးထားသော Array တွင် binary ရှာဖွေမှုကို လုပ်ဆောင်သည့် 'binarySearch ()' နည်းလမ်းကို ပံ့ပိုးပေးပါသည်။ ဤနည်းလမ်းသည် array နှင့် key ကို arguments များအဖြစ် ရှာဖွေရန်နှင့် array ရှိ key ၏ အနေအထားကို ပြန်ပေးသည်။ သော့ကို ရှာမတွေ့ပါက၊ နည်းလမ်းသည် -1 ကို ပြန်ပေးသည်။
အောက်ပါ ဥပမာသည် Arrays.binarySearch () နည်းလမ်းကို အကောင်အထည် ဖော်သည်။
import java.util.Arrays; class Main{ public static void main(String args[]){ //define an array int intArray[] = {10,20,30,40,50,60,70,80,90}; System.out.println("The input Array : " + Arrays.toString(intArray)); //define the key to be searched int key = 50; System.out.println("\nThe key to be searched:" + key); //call binarySearch method on the given array with key to be searched int result = Arrays.binarySearch(intArray,key); //print the return result if (result 0) System.out.println("\nKey is not found in the array!"); else System.out.println("\nKey is found at index: "+result + " in the array."); } } Output-
ထည့်သွင်းသည့် Array : [10၊ 20၊ 30၊ 40၊ 50၊ 60၊ 70၊ 80၊ 90]
ရှာဖွေရမည့်သော့ :50
ကီးကို အညွှန်း- 4 ကို array တွင်တွေ့နိုင်သည်။
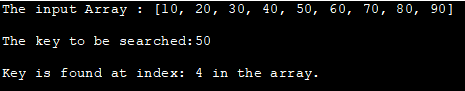
အမေးများသောမေးခွန်းများ
Q #1) binary ရှာဖွေမှုကို သင်မည်သို့ရေးပါသနည်း။ ?
အဖြေ- Binary ရှာဖွေမှုကို အများအားဖြင့် array ကို တစ်ဝက်ခွဲ၍ လုပ်ဆောင်သည်။ ရှာဖွေရမည့်သော့သည် အလယ်ဒြပ်ထက်ကြီးပါက၊ထို့နောက် သော့ကိုမတွေ့မချင်း array ၏အပေါ်ပိုင်းတစ်ဝက်ကို ထပ်မံခွဲခြမ်းပြီး ရှာဖွေခြင်းဖြင့် ရှာဖွေမည်ဖြစ်သည်။
ထို့အတူ သော့သည် အလယ်ဒြပ်စင်ထက်နည်းပါက၊ အောက်ခြေတွင် သော့ကိုရှာဖွေမည်ဖြစ်သည်။ array ၏ ထက်ဝက်။
မေး #2) Binary ရှာဖွေမှုကို မည်သည့်နေရာတွင် အသုံးပြုသနည်း။
အဖြေ- Binary ရှာဖွေမှုကို အဓိကအားဖြင့် ရှာဖွေရန် အသုံးပြုပါသည်။ အထူးသဖြင့် မမ်မိုရီနေရာများ ကျစ်လျစ်ပြီး အကန့်အသတ်ရှိသည့်အခါ ဆော့ဖ်ဝဲအပလီကေးရှင်းများတွင် ဒေတာများကို စီတန်းထားသည်။
မေး #3) binary ရှာဖွေမှု၏ ကြီးမားသော O မှာ အဘယ်နည်း။
အဖြေ : ဒွိရှာဖွေမှု၏ အချိန်ရှုပ်ထွေးမှုသည် O (logn) ဖြစ်ပြီး array ရှိ ဒြပ်စင်အရေအတွက် N သည် O (logn) ဖြစ်သည်။ ဒွိစုံရှာဖွေမှု၏ အာကာသရှုပ်ထွေးမှုသည် O (1) ဖြစ်သည်။
မေးခ #4) ဒွိစုံရှာဖွေမှု ထပ်တူကျပါသလား။
အဖြေ- ဟုတ်ကဲ့။ ဒွိစုံရှာဖွေမှုသည် ခွဲဝေရယူခြင်းဗျူဟာ၏ ဥပမာတစ်ခုဖြစ်ပြီး ၎င်းကို recursion ဖြင့် အကောင်အထည်ဖော်နိုင်သည်။ array ကို တစ်ဝက်ခွဲပြီး binary ရှာဖွေမှုကို ထပ်ခါထပ်ခါ လုပ်ဆောင်ရန် တူညီသောနည်းလမ်းကို ခေါ်နိုင်သည်။
မေး #5) အဘယ်ကြောင့် ၎င်းကို binary ရှာဖွေမှုဟု ခေါ်သနည်း။
အဖြေ- ဒွိရှာဖွေမှု အယ်လဂိုရီသမ်သည် array အား အပိုင်း (သို့) နှစ်ပိုင်းသို့ ထပ်ခါတလဲလဲ ဖြတ်တောက်သည့် ခွဲခြမ်းနှင့် အနိုင်ယူနည်းဗျူဟာကို အသုံးပြုသည်။ ထို့ကြောင့် ၎င်းကို binary ရှာဖွေမှုဟု အမည်ပေးထားသည်။
နိဂုံး
Binary search သည် Java တွင် မကြာခဏအသုံးပြုသော ရှာဖွေရေးနည်းပညာဖြစ်သည်။ ဒွိစုံရှာဖွေမှုတစ်ခုလုပ်ဆောင်ရန် လိုအပ်ချက်မှာ ဒေတာကို ကြီးလိုက်ကြီးလိုက် စီထားသင့်သည်။
ဒွိစုံရှာဖွေမှုတစ်ခု ဖြစ်နိုင်သည်။ထပ်ခါထပ်ခါ သို့မဟုတ် ထပ်ခါတလဲလဲ ချဉ်းကပ်နည်းကို အသုံးပြု၍ အကောင်အထည်ဖော်ခဲ့သည်။ Java ရှိ Arrays အတန်းသည် Array တစ်ခုပေါ်တွင် binary ရှာဖွေမှုကို လုပ်ဆောင်သည့် 'binarySearch' နည်းလမ်းကိုလည်း ပံ့ပိုးပေးပါသည်။
ကျွန်ုပ်တို့၏နောက်ဆက်တွဲသင်ခန်းစာများတွင်၊ Java ရှိ အမျိုးအစားခွဲခြင်းနည်းပညာအမျိုးမျိုးကို လေ့လာပါမည်။