学习如何使用Python中的Sort函数对列表、数组、字典等进行排序,使用Python中的各种排序方法和算法:
排序是一种技术,用于按照升序或降序的顺序对数据进行排序。
大多数时候,大型项目的数据没有按照正确的顺序排列,这在有效访问和获取所需数据时产生了问题。
分拣技术被用来解决这个问题。 Python提供了各种分拣技术 例如: 泡沫排序、插入排序、合并排序、快速排序等。
在本教程中,我们将通过使用各种算法了解Python中的排序工作。
Python排序

Python排序的语法
为了进行排序,Python提供了内置函数,即 "sort() "函数。 它被用来对列表中的数据元素按升序或降序进行排序。
让我们通过一个例子来理解这个概念。
例1:
```a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( " List in ascending order: ", a ) ```.
输出:

在这个例子中,通过使用" sort( ) "函数将给定的无序列表排序为升序。
例2:
```a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( " List in descending order: ", a ) ```.
输出

在上面的例子中,使用函数" sort( reverse = True ) "对给定的无序列表进行反向排序。
排序算法的时间复杂度
时间复杂度是指计算机运行一个特定算法所需的时间。 它有三种类型的时间复杂度情况。
- 最坏的情况: 计算机运行程序所需的最大时间。
- 平均案例: 计算机运行程序所需的最小和最大之间的时间。
- 最佳案例: 计算机运行程序所需的最小时间。 它是时间复杂性的最佳情况。
复杂度记号
大O记号,O: Big oh符号是表达算法运行时间上限的正式方式。 它被用来衡量最坏情况下的时间复杂度,或者我们说算法完成所需的最大时间量。
大欧米茄记号、  : Big omega符号是传达算法运行时间最低界限的正式方式。 它被用来衡量最佳情况下的时间复杂度,或者我们说算法所花费的优秀时间量。
: Big omega符号是传达算法运行时间最低界限的正式方式。 它被用来衡量最佳情况下的时间复杂度,或者我们说算法所花费的优秀时间量。
Theta记号、 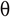 : Theta符号是表达两种界限的正式方式,即算法完成所需时间的下限和上限。
: Theta符号是表达两种界限的正式方式,即算法完成所需时间的下限和上限。
Python中的排序方法
泡沫分类
泡沫排序是最简单的数据排序方法,它使用暴力技术。 它将对每个数据元素进行迭代,并与其他元素进行比较,为用户提供排序后的数据。
让我们举个例子来理解这种技术:
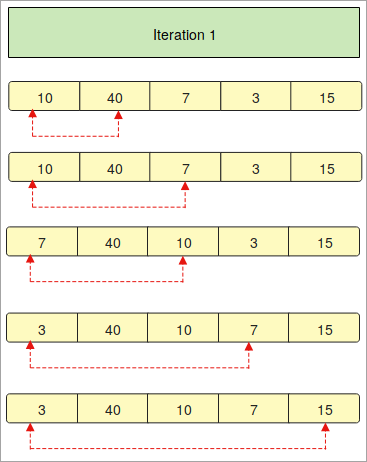
- 我们得到一个元素为 "10, 40, 7, 3, 15 "的数组,现在,我们需要使用Python中的泡沫排序技术将这个数组按升序排列。
- 第一步是按照给定的顺序排列数组。
- 在 "迭代1 "中,我们将一个数组的第一个元素与其他元素逐一进行比较。
- 红色箭头描述的是第一个元素与数组中其他元素的比较。
- 如果你注意到 "10 "比 "40 "小,所以它仍然在同一位置,但下一个元素 "7 "比 "10 "小,因此它被替换到了第一位置。
- 上述过程将被反复执行,以对元素进行排序。
- 在 "迭代2 "中,第二个元素正在与数组的其他元素进行比较。
- 如果被比较的元素是小的,那么它将被替换,否则它将保持在同一位置。

- 在 "迭代3 "中,第三个元素正在与数组的其他元素进行比较。

- 在最后的 "迭代4 "中,倒数第二个元素与数组的其他元素进行比较。
- 在这一步中,数组被按升序排序。

泡沫分类的程序
`` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Unorted List: " , unsorted_list) print("Sorted List using Bubble SortTechnique: ", Bubble_Sort(unsorted_list)) ````。 输出

泡沫排序的时间复杂度
- 最坏的情况: 冒泡排序的最差时间复杂度是O( n 2).
- 平均案例: 冒泡排序的平均时间复杂度为O( n 2).
- 最佳案例: 冒泡排序的最佳时间复杂度是O(n)。
优势
- 它大多被使用,而且很容易实现。
- 我们可以在不消耗短期存储的情况下交换数据元素。
- 它需要更少的空间。
劣势
- 在处理大量的大数据元素时,它的表现并不理想。
- 它需要 n 对每一个 "n "个数据元素进行排序,需要2个步骤。
- 它对现实世界的应用并不真正有利。
插入排序
插入式排序是一种简单易行的排序技术,其工作原理类似于扑克牌的排序。 插入式排序通过将每个元素逐一与其他元素进行比较来进行排序。 如果元素大于或小于另一个元素,则将该元素挑出并与另一个元素进行交换。
让我们举个例子
- 我们得到了一个元素为 "100, 50, 30, 40, 10 "的数组。
- 首先,我们排列数组并开始比较。
- 在第一步中,"100 "与第二个元素 "50 "进行比较。"50 "与 "100 "互换,因为它更大。
- 在第二步中,第二元素 "100 "再次与第三元素 "30 "进行比较并被交换。
- 现在,如果你注意到 "30 "排在第一位,因为它又比 "50 "小。
- 比较将一直发生到数组的最后一个元素,在最后,我们将得到排序后的数据。

插入排序的程序
`` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j>= 0 and key_value <array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("The unsorted array: ", array) InsertionSort(array) print("The sorted array using the Insertion Sort: ") for i in range(len(array)): print (array[i] ) `` ` 输出
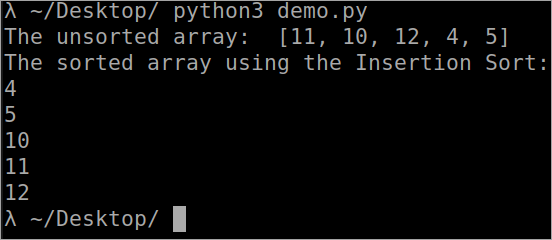
插入排序的时间复杂度
- 最坏的情况: 插入式排序的最差时间复杂度是O( n 2).
- 平均案例: 插入式排序的平均时间复杂度为O( n 2).
- 最佳案例: 插入式排序的最佳时间复杂度是O(n)。
优势
- 它很简单,易于实施。
- 它在处理少量数据元素时表现良好。
- 它不需要更多的空间来实施。
劣势
- 对大量的数据元素进行分类是没有帮助的。
- 与其他分拣技术相比,它的表现并不理想。
合并排序
这种排序方法使用分而治之的方法将元素按特定顺序进行排序。 在合并排序的帮助下,元素被分成两半,然后被排序。 在对所有两半进行排序后,元素再次被连接起来,形成一个完美的顺序。
让我们举个例子来理解这个技术
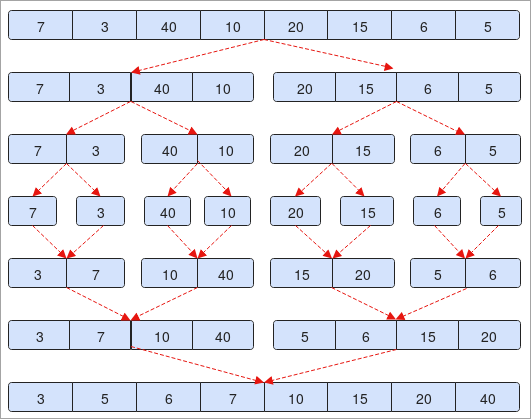
- 我们得到一个数组 "7,3,40,10,20,15,6,5"。 该数组包含7个元素。 如果我们把它分成一半(0 + 7 / 2 = 3)。
- 在第二步中,你会看到元素被分为两部分。 每部分有4个元素。
- 进一步说,这些元素再次被划分,每个元素有2个。
- 这个过程将持续到数组中只有一个元素为止。 请参考图片中的第4步。
- 现在,我们将对这些元素进行分类,并开始按照我们的划分来连接它们。
- 在第5步中,如果你注意到7大于3,那么我们将交换它们并在下一步中加入,反之亦然。
- 最后,你会注意到,我们的数组正按升序排序。
合并排序的程序
``` def MergeSort(arr): if len(arr)> 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i <len(L) and j <len(R): if L[i] <R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i <len(L): arr[k] = L[i] i += 1 k += 1 while j <len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i inrange(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Given array is", end="\n") PrintSortedList(arr) MergeSort(arr) print("Sorted array is: ", end="\n") PrintSortedList(arr) ````。 输出
合并排序的时间复杂度
- 最坏的情况: 合并排序的最差时间复杂度是O( n log( n )).
- 平均案例: 合并排序的平均时间复杂度为O( n log( n )).
- 最佳案例: 合并排序的最佳时间复杂度是O( n log( n )).
优势
- 对于这种排序技术,文件大小并不重要。
- 这种技术适用于一般按顺序访问的数据。 比如说、 链表、磁带机等。
劣势
- 与其他分拣技术相比,它需要更多空间。
- 它的效率相对来说比其他的要低。
快速排序
快速排序再次使用分而治之的方法对List或数组中的元素进行排序。 它以枢轴元素为目标,根据选定的枢轴元素对元素进行排序。
比如说
- 我们得到了一个数组,其元素为 "1,8,3,9,4,5,7"。
- 让我们假设 " 7 " 是一个试点元素。
- 现在我们将以这样的方式划分数组,左边包含小于枢轴元素" 7 "的元素,右边包含大于枢轴元素" 7 "的元素。
- 我们现在有两个数组 " 1,3,4,5 " 和 " 8, 9 " 。
- 同样,我们必须像上面那样对两个数组进行分割。 唯一的区别是,枢轴元素被改变。
- 我们需要对数组进行分割,直到得到数组中的单个元素。
- 最后,按顺序从左到右收集所有的枢轴元素,你将得到排序后的数组。
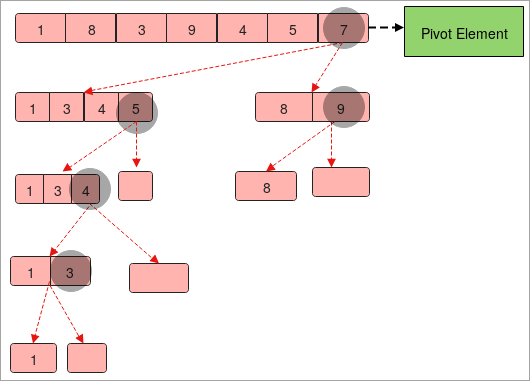
快速排序的程序
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] <= pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ) return ( i+1 ) def QuickSort( arr, lowest, highest ) : if len( arr ) == 1: return arr if lowest <highest: pi = Array_Partition(arr, lowest, highest ) QuickSort( arr, lowest, pi-1 ) QuickSort( arr, pi+1, highest ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Unsorted array: ", arr ) QuickSort( arr, 0, n-1 ) print( " Sorted array using Quick Sort: " ) for i in range( n ): print( " %d " % arr[ i ] ) ````
输出
快速排序的时间复杂度
- 最坏的情况: 快速排序的最差时间复杂度是O( n 2).
- 平均案例: 快速排序的平均时间复杂度为O( n log( n )).
- 最佳案例: 快速排序的最佳时间复杂度是O( n log( n )).
优势
- 它被称为Python中最好的排序算法。
- 在处理大量数据时,它很有用。
- 它不需要额外的空间。
劣势
- 其最坏情况下的复杂度与冒泡排序和插入排序的复杂度相似。
- 当我们已经有了排序后的列表,这种排序方法就没有用了。
堆积排序
堆排序是二进制搜索树的高级版本。 在堆排序中,数组中最大的元素总是放在树的根部,然后,与根部和叶子节点进行比较。
比如说:
- 我们得到了一个元素为 "40、100、30、50、10 "的数组。
- 在 " 第1步 " 我们根据数组中元素的存在做了一棵树。

- 在" 第2步" 我们要做一个最大的堆,即按降序排列元素。 最大的元素将位于顶部(根节点),最小的元素位于底部(叶节点)。 给定的数组成为 "100, 50, 30, 40, 10"。

- 在 " 第三步 " 通过这样做,我们可以得到最大和最小的元素。

- 在 " 第四步 " 通过执行同样的步骤,我们得到了排序后的数组。

堆积排序的程序
`` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left <n and arr[ larger_element ] <arr[ left ]: larger_element = left if right <n and arr[ larger_element ] <arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ) def HeapSortify( arr, n, larger_element )): n = len( arr ) for i in range( n/2 - 1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " The unsorted array is: ", arr ) HeapSort( arr ) n = len( arr ) print( " The sorted array sorted by heap sort: " ) for i in range( n ) : print( arr[ i ] ) ````
输出
堆积排序的时间复杂度
- 最坏的情况: 堆排序的最差时间复杂度是O( n log( n )).
- 平均案例: Heap排序的平均时间复杂度为O( n log( n )).
- 最佳案例: 堆排序的最佳时间复杂度是O( n log( n )).
优势
- 它之所以被使用,主要是因为它的生产力。
- 它可以作为一种就地的算法来实现。
- 它不需要大量的存储。
劣势
- 需要空间来对元素进行分类。
- 它使元素分类的树。
分拣技术的比较
| 分拣方法 | 最佳情况下的时间复杂性 | 平均案件时间复杂度 | 最坏情况下的时间复杂性 | 空间的复杂性 | 稳定性 | 在-地方 |
|---|---|---|---|---|---|---|
| 泡沫排序 | O(n) | O(n2) | O(n2) | O(1) | 是 | 是 |
| 插入式排序 | O(n) | O(n2) | O(n2) | O(1) | 是 | 是 |
| 快速排序 | O(n log(n)) | O(n log(n)) | O(n2) | O(N) | 没有 | 是 |
| 合并排序 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(N) | 是 | 没有 |
| 堆积排序 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) | 没有 | 是 |
在上面的比较表中,"O "是上面解释的大O的符号,而 "n "和 "N "是指输入的大小。
常见问题
问题#1) Python中的sort()是什么?
答案是: 在Python中,sort()是一个用于按特定顺序对列表或数组进行排序的函数。 这个函数简化了在大型项目中进行排序的过程。 它对开发人员非常有帮助。
Q #2) 在Python中如何排序?
答案是: Python提供了各种排序技术,用于对元素进行排序。 比如说、 快速排序、合并排序、气泡排序、插入排序等,所有的排序技术都是高效且易于理解的。
问题#3) Python sort ()是如何工作的?
答案是: sort()函数将给定的数组作为用户的输入,并使用排序算法对其进行特定的排序。 算法的选择取决于用户的选择。 用户可以使用快速排序、合并排序、泡沫排序、插入排序等,这取决于用户的需求。
总结
在上面的教程中,我们讨论了Python中的排序技术,以及一般的排序技术。
- 泡沫分类
- 插入排序
- 快速排序
我们了解了他们的时间复杂性和优点及缺点。 我们还比较了上述所有技术。