Naučte sa používať funkciu Python Sort na triedenie zoznamov, polí, slovníkov atď. pomocou rôznych metód a algoritmov triedenia v jazyku Python:
Triedenie je technika, ktorá sa používa na zoradenie údajov v poradí buď vzostupne, alebo zostupne.
Údaje veľkých projektov väčšinou nie sú usporiadané v správnom poradí, čo spôsobuje problémy pri efektívnom prístupe k požadovaným údajom a ich načítavaní.
Na vyriešenie tohto problému sa používajú techniky triedenia. Python poskytuje rôzne techniky triedenia napríklad, Bubble sort, Insertion sort, Merge sort, Quicksort atď.
V tomto učebnom texte pochopíme, ako funguje triedenie v jazyku Python pomocou rôznych algoritmov.
Triedenie v jazyku Python

Syntax jazyka Python Sort
Na triedenie poskytuje Python vstavanú funkciu, t. j. funkciu " sort() ". Používa sa na triedenie dátových prvkov zoznamu vo vzostupnom alebo zostupnom poradí.
Pochopme tento koncept na príklade.
Príklad 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( " Zoznam vo vzostupnom poradí: ", a ) ```
Výstup:

V tomto príklade je daný neusporiadaný zoznam zoradený vzostupne pomocou funkcie " sort( ) ".
Príklad 2:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( " Zoznam v zostupnom poradí: ", a ) ```
Výstup

V uvedenom príklade je daný neusporiadaný zoznam zoradený v opačnom poradí pomocou funkcie " sort( reverse = True ) ".
Časová zložitosť triediacich algoritmov
Časová zložitosť je množstvo času, ktoré počítač potrebuje na spustenie určitého algoritmu. Má tri typy prípadov časovej zložitosti.
- Najhorší prípad: Maximálny čas, ktorý počítač potrebuje na spustenie programu.
- Priemerný prípad: Čas, ktorý počítač potrebuje na spustenie programu medzi minimom a maximom.
- Najlepší prípad: Minimálny čas, ktorý počítač potrebuje na spustenie programu. Je to najlepší prípad časovej zložitosti.
Zápisy zložitosti
Big Oh Notation, O: Zápis Big Oh je oficiálny spôsob vyjadrenia hornej hranice času behu algoritmov. Používa sa na meranie časovej zložitosti v najhoršom prípade alebo hovoríme o najväčšom čase, ktorý algoritmus potrebuje na dokončenie.
Veľká omega Notácia,  : Zápis veľká omega je oficiálny spôsob, ako vyjadriť najnižšiu hranicu času behu algoritmov. Používa sa na meranie časovej zložitosti v najlepšom prípade alebo hovoríme o vynikajúcom množstve času, ktoré algoritmus potrebuje.
: Zápis veľká omega je oficiálny spôsob, ako vyjadriť najnižšiu hranicu času behu algoritmov. Používa sa na meranie časovej zložitosti v najlepšom prípade alebo hovoríme o vynikajúcom množstve času, ktoré algoritmus potrebuje.
Theta notácia, 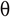 : Theta zápis je oficiálny spôsob, ako vyjadriť obe hranice, t. j. dolnú a hornú hranicu času potrebného na dokončenie algoritmu.
: Theta zápis je oficiálny spôsob, ako vyjadriť obe hranice, t. j. dolnú a hornú hranicu času potrebného na dokončenie algoritmu.
Metódy triedenia v jazyku Python
Bublinové triedenie
Bubble sort je najjednoduchší spôsob triedenia údajov, ktorý využíva techniku hrubej sily. Iteruje každý dátový prvok a porovnáva ho s ostatnými prvkami, aby poskytol používateľovi zoradené údaje.
Poďme si túto techniku vysvetliť na príklade:
- Máme k dispozícii pole s prvkami " 10, 40, 7, 3, 15 ". Teraz musíme toto pole usporiadať vzostupne pomocou techniky Bubble sort v jazyku Python.
- Prvým krokom je usporiadanie poľa v danom poradí.
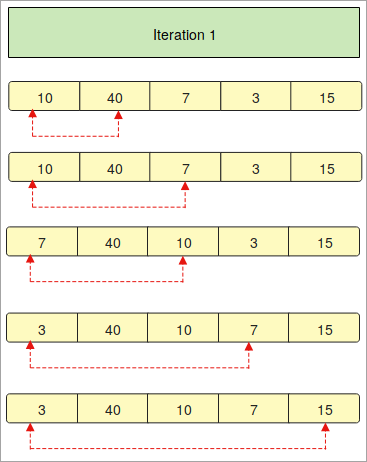
- V "Iterácii 1" porovnávame prvý prvok poľa s ostatnými prvkami jeden po druhom.
- Červené šípky popisujú porovnanie prvých prvkov s ostatnými prvkami poľa.
- Ak si všimnete, že prvok " 10 " je menší ako prvok " 40 ", zostáva na rovnakom mieste, ale ďalší prvok " 7 " je menší ako prvok " 10 ". Preto sa nahradí a dostane sa na prvé miesto.
- Vyššie uvedený postup sa bude opakovať, aby sa prvky zoradili.
- V " Iterácii 2 " sa druhý prvok porovnáva s ostatnými prvkami poľa.
- Ak je porovnávaný prvok malý, nahradí sa, inak zostane na rovnakom mieste.

- V " Iterácii 3 " sa tretí prvok porovnáva s ostatnými prvkami poľa.

- V poslednej " Iterácii 4 " sa predposledný prvok porovnáva s ostatnými prvkami poľa.
- V tomto kroku sa pole zoradí vzostupne.

Program pre Bubble sort
``` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Neusporiadaný zoznam: ", unsorted_list) print("Usporiadaný zoznam pomocou Bubble SortTechnika: ", Bubble_Sort(unsorted_list)) ``` Výstup

Časová zložitosť triedenia bublín
- Najhorší prípad: Najhoršia časová zložitosť pre bublinové triedenie je O( n 2).
- Priemerný prípad: Priemerná časová zložitosť bublinového triedenia je O( n 2).
- Najlepší prípad: Najlepšia časová zložitosť pre bubble sort je O(n).
Výhody
- Väčšinou sa používa a je ľahko implementovateľný.
- Dátové prvky môžeme vymieňať bez spotreby krátkodobého úložiska.
- Vyžaduje si menej miesta.
Nevýhody
- Pri práci s veľkým počtom veľkých dátových prvkov sa neosvedčil.
- Potrebuje n 2 kroky pre každý "n" počet dátových prvkov, ktoré sa majú zoradiť.
- Na reálne aplikácie nie je veľmi vhodný.
Triedenie vkladania
Insertion sort je jednoduchá a ľahká technika triedenia, ktorá funguje podobne ako triedenie hracích kariet. Insertion sort triedi prvky tak, že porovnáva jednotlivé prvky jeden po druhom. Prvky sa vyberú a vymenia s iným prvkom, ak je prvok väčší alebo menší ako druhý.
Uveďme si príklad
- Máme k dispozícii pole s prvkami " 100, 50, 30, 40, 10 ".
- Najprv usporiadame pole a začneme ho porovnávať.
- V prvom kroku sa prvok " 100 " porovná s druhým prvkom " 50 ". 50 " sa vymení za 100 ", pretože je väčší.
- V druhom kroku sa opäť porovná druhý prvok " 100 " s tretím prvkom " 30 " a vymení sa.
- Ak si všimnete, na prvom mieste je "30", pretože je opäť menšia ako "50".
- Porovnávanie bude prebiehať až po posledný prvok poľa a na konci dostaneme zoradené údaje.

Program na triedenie vkladania
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j>= 0 and key_value <array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("Netriedené pole: ", array) InsertionSort(array) print ("Triedené pole pomocou Insertion Sort: ") for i in range(len(array)): print (array[i]) ``` Výstup
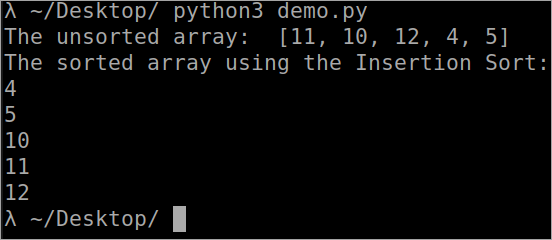
Časová zložitosť triedenia vkladania
- Najhorší prípad: Najhoršia časová zložitosť pre Insertion sort je O( n 2).
- Priemerný prípad: Priemerná časová zložitosť triedenia Insertion je O( n 2).
- Najlepší prípad: Najlepšia časová zložitosť pre Insertion sort je O(n).
Výhody
- Je jednoduchý a ľahko sa implementuje.
- Dobre pracuje s malým počtom dátových prvkov.
- Na svoju realizáciu nepotrebuje viac priestoru.
Nevýhody
- Nie je užitočné triediť obrovské množstvo dátových prvkov.
- V porovnaní s inými technikami triedenia nemá dobré výsledky.
Zlúčenie triedenia
Táto metóda triedenia využíva metódu rozdeľ a panuj na zoradenie prvkov v určitom poradí. Pri triedení pomocou merge sort sa prvky rozdelia na polovice a potom sa zoradia. Po zoradení všetkých polovíc sa prvky opäť spoja, aby vytvorili dokonalé poradie.
Uveďme si príklad, aby sme pochopili túto techniku
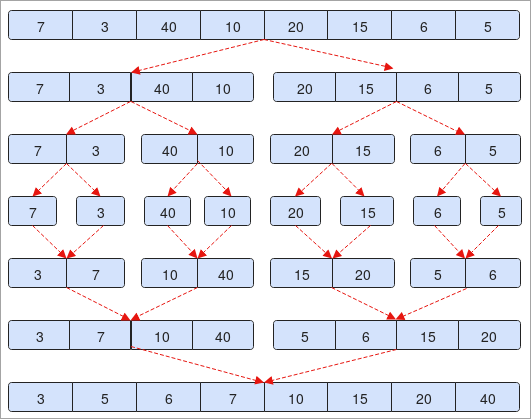
- Máme k dispozícii pole " 7, 3, 40, 10, 20, 15, 6, 5 ". Pole obsahuje 7 prvkov. Ak ho rozdelíme na polovicu ( 0 + 7 / 2 = 3 ).
- V druhom kroku uvidíte, že prvky sú rozdelené na dve časti. Každá z nich má 4 prvky.
- Ďalej sú prvky opäť rozdelené a každý má 2 prvky.
- Tento proces bude pokračovať, kým v poli nebude iba jeden prvok. Pozrite si krok č. 4 na obrázku.
- Teraz prvky roztriedime a začneme ich spájať tak, ako sme ich rozdelili.
- Ak si v kroku č. 5 všimnete, že 7 je väčšie ako 3, tak si ich v ďalšom kroku vymeníme a spojíme a naopak.
- Na konci si všimnete, že naše pole sa zoradí vzostupne.
Program na triedenie Merge
``` def MergeSort(arr): if len(arr)> 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i <len(L) and j <len(R): if L[i] <R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i <len(L): arr[k] = L[i] i += 1 k += 1 while j <len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i inrange(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Dané pole je", end="\n") PrintSortedList(arr) MergeSort(arr) print("Zoradené pole je: ", end="\n") PrintSortedList(arr) ``` Výstup
Časová zložitosť zlučovania
- Najhorší prípad: Najhoršia časová zložitosť pre merge sort je O( n log( n )).
- Priemerný prípad: Priemerná časová zložitosť zlučovania je O( n log( n )).
- Najlepší prípad: Najlepšia časová zložitosť pre merge sort je O( n log( n )).
Výhody
- Pri tejto technike triedenia nezáleží na veľkosti súboru.
- Táto technika je vhodná pre údaje, ku ktorým sa vo všeobecnosti pristupuje v postupnom poradí. Napríklad, prepojené zoznamy, pásková jednotka atď.
Nevýhody
- V porovnaní s inými technikami triedenia si vyžaduje viac miesta.
- Je relatívne menej účinný ako ostatné.
Rýchle triedenie
Rýchle triedenie opäť používa metódu rozdeľ a panuj na triedenie prvkov zoznamu alebo poľa. Zameriava sa na otočné prvky a triedi prvky podľa vybraného otočného prvku.
Napríklad
- Máme k dispozícii pole s prvkami " 1,8,3,9,4,5,7 ".
- Predpokladajme, že " 7 " je pilotný prvok.
- Teraz rozdelíme pole tak, aby ľavá strana obsahovala prvky, ktoré sú menšie ako otočný prvok " 7 ", a pravá strana obsahovala prvky väčšie ako otočný prvok " 7 ".
- Teraz máme dve polia " 1,3,4,5 " a " 8, 9 ".
- Opäť musíme obe polia rozdeliť rovnako, ako sme to urobili vyššie. Jediný rozdiel je v tom, že sa zmenia otočné prvky.
- Musíme rozdeliť polia, kým nezískame jediný prvok v poli.
- Na konci zozbierajte všetky otočné prvky v poradí zľava doprava a získate zoradené pole.
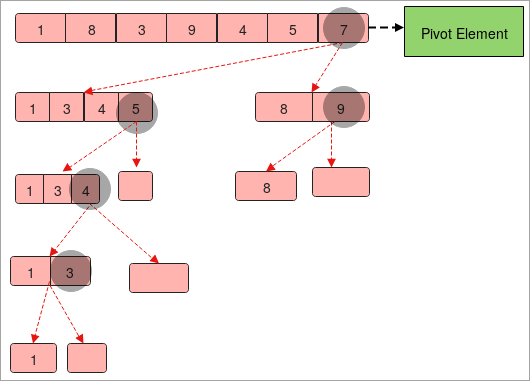
Program pre rýchle triedenie
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] <= pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i ] arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ] return ( i+1 ) def QuickSort( arr, lowest, highest ): if len( arr ) == 1: return arr if lowest <highest: pi = Array_Partition(arr, najnižšia, najvyššia ) QuickSort( arr, najnižšia, pi-1 ) QuickSort( arr, pi+1, najvyššia ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Unsorted array: ", arr ) QuickSort( arr, 0, n-1 ) print( " Sorted array using Quick Sort: " ) for i in range( n ): print( " %d " % arr[ i ] ) ```
Výstup
Časová náročnosť rýchleho triedenia
- Najhorší prípad: Najhoršia časová zložitosť pre Quick sort je O( n 2).
- Priemerný prípad: Priemerná časová zložitosť pre rýchle triedenie je O( n log( n )).
- Najlepší prípad: Najlepšia časová zložitosť pre Quick sort je O( n log( n )).
Výhody
- Je známy ako najlepší triediaci algoritmus v jazyku Python.
- Je užitočný pri spracovaní veľkého množstva údajov.
- Nevyžaduje si ďalší priestor.
Nevýhody
- Jeho zložitosť v najhoršom prípade je podobná zložitosti bubble sort a insertion sort.
- Táto metóda triedenia nie je užitočná, ak už máme zoradený zoznam.
Triedenie na hromadu
Hromadné triedenie je pokročilá verzia binárneho vyhľadávacieho stromu. Pri hromadnom triedení sa najväčší prvok poľa umiestni vždy na koreň stromu a potom sa porovná s koreňom s listovými uzlami.
Napríklad:
- Máme k dispozícii pole s prvkami " 40, 100, 30, 50, 10 ".
- Na stránke " krok 1 " sme vytvorili strom podľa prítomnosti prvkov v poli.

- V " krok 2 " vytvárame maximálnu hromadu, t. j. usporiadanie prvkov v zostupnom poradí. Najväčší prvok sa bude nachádzať na vrchu (koreň) a najmenší prvok sa bude nachádzať na spodku (listové uzly). Dané pole sa stáva " 100, 50, 30, 40, 10 ".

- Na stránke " krok 3 " , vytvárame minimálnu hromadu, aby sme mohli nájsť minimálne prvky poľa. Týmto spôsobom získame maximálne a minimálne prvky.

- Na stránke " krok 4 " vykonaním rovnakých krokov získame zoradené pole.

Program pre triedenie na hromadu
``` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left <n and arr[ larger_element ] <arr[ left ]: larger_element = left if right <n and arr[ larger_element ] <arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ] HeapSortify( arr, n, larger_element ) def HeapSort( arr): n = len( arr ) for i in range( n//2 - 1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " Nezoradené pole je: ", arr ) HeapSort( arr ) n = len( arr ) print( " Zoradené pole zoradené pomocou Heap Sort: " ) for i in range( n ): print( arr[ i ] ) ```
Výstup
Časová zložitosť triedenia na hromadách
- Najhorší prípad: Najhoršia časová zložitosť pre triedenie na hromade je O( n log( n )).
- Priemerný prípad: Priemerná časová zložitosť triedenia na hromade je O( n log( n )).
- Najlepší prípad: Najlepšia časová zložitosť pre triedenie na hromade jeO( n log( n )).
Výhody
- Používa sa najmä vďaka svojej produktivite.
- Možno ho implementovať ako algoritmus na mieste.
- Nevyžaduje veľké úložisko.
Nevýhody
- Potrebuje priestor na triedenie prvkov.
- Vytvára strom na triedenie prvkov.
Porovnanie techník triedenia
| Metóda triedenia | Časová zložitosť v najlepšom prípade | Priemerná časová zložitosť prípadu | Najhoršia časová zložitosť | Priestorová zložitosť | Stabilita | Na mieste |
|---|---|---|---|---|---|---|
| Bublinkové triedenie | O(n) | O(n2) | O(n2) | O(1) | Áno | Áno |
| Triedenie vkladania | O(n) | O(n2) | O(n2) | O(1) | Áno | Áno |
| Rýchle triedenie | O(n log(n)) | O(n log(n)) | O(n2) | O(N) | Nie | Áno |
| Zlúčenie triedenia | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(N) | Áno | Nie |
| Triedenie na hromadu | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) | Nie | Áno |
Vo vyššie uvedenej porovnávacej tabuľke " O " je vysvetlený zápis Big Oh, zatiaľ čo " n " a " N " znamená veľkosť vstupu.
Často kladené otázky
Otázka č. 1) Čo je to sort () v jazyku Python?
Odpoveď: V jazyku Python je funkcia sort(), ktorá sa používa na triedenie zoznamov alebo polí v určitom poradí. Táto funkcia uľahčuje proces triedenia pri práci na veľkých projektoch. Je veľmi užitočná pre vývojárov.
Otázka č. 2) Ako triedite v jazyku Python?
Odpoveď: Python poskytuje rôzne techniky triedenia, ktoré sa používajú na triedenie prvkov. Napríklad, Rýchle triedenie, Zlúčené triedenie, Bublinkové triedenie, Vložené triedenie atď. Všetky techniky triedenia sú efektívne a ľahko pochopiteľné.
Q #3) Ako funguje triedenie () v jazyku Python?
Odpoveď: Funkcia sort() prevezme zadané pole ako vstup od používateľa a zoradí ho v určitom poradí pomocou triediaceho algoritmu. Výber algoritmu závisí od voľby používateľa. Používateľ môže použiť Quick sort, Merge sort, Bubble sort, Insertion sort atď. v závislosti od potrieb používateľa.
Záver
Vo vyššie uvedenom návode sme sa venovali technike triedenia v jazyku Python spolu so všeobecnými technikami triedenia.
- Bublinové triedenie
- Triedenie vkladania
- Rýchle triedenie
Dozvedeli sme sa o ich časovej náročnosti a výhodách & nevýhodách. Všetky uvedené techniky sme tiež porovnali.