ಪೈಥಾನ್ನಲ್ಲಿ ವಿವಿಧ ವಿಂಗಡಣೆ ವಿಧಾನಗಳು ಮತ್ತು ಅಲ್ಗಾರಿದಮ್ಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಪಟ್ಟಿಗಳು, ಅರೇಗಳು, ನಿಘಂಟುಗಳು, ಇತ್ಯಾದಿಗಳನ್ನು ವಿಂಗಡಿಸಲು ಪೈಥಾನ್ ವಿಂಗಡಣೆ ಕಾರ್ಯವನ್ನು ಹೇಗೆ ಬಳಸುವುದು ಎಂದು ತಿಳಿಯಿರಿ:
ವಿಂಗಡಣೆಯು ವಿಂಗಡಣೆಗಾಗಿ ಬಳಸಲಾಗುವ ತಂತ್ರವಾಗಿದೆ ದತ್ತಾಂಶವು ಆರೋಹಣ ಅಥವಾ ಅವರೋಹಣ ಕ್ರಮದಲ್ಲಿ ಅನುಕ್ರಮ ಕ್ರಮದಲ್ಲಿ.
ಹೆಚ್ಚಾಗಿ ದೊಡ್ಡ ಯೋಜನೆಗಳ ಡೇಟಾವನ್ನು ಸರಿಯಾದ ಕ್ರಮದಲ್ಲಿ ಜೋಡಿಸಲಾಗಿಲ್ಲ ಮತ್ತು ಇದು ಅಗತ್ಯವಿರುವ ಡೇಟಾವನ್ನು ಸಮರ್ಥವಾಗಿ ಪ್ರವೇಶಿಸುವಾಗ ಮತ್ತು ಪಡೆಯುವಲ್ಲಿ ಸಮಸ್ಯೆಗಳನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ.
ವಿಂಗಡಣೆ ತಂತ್ರಗಳನ್ನು ಈ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ. ಪೈಥಾನ್ ವಿವಿಧ ವಿಂಗಡಣೆ ತಂತ್ರಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ ಉದಾಹರಣೆಗೆ, ಬಬಲ್ ವಿಂಗಡಣೆ, ಅಳವಡಿಕೆ ವಿಂಗಡಣೆ, ವಿಲೀನ ವಿಂಗಡಣೆ, ಕ್ವಿಕ್ಸಾರ್ಟ್, ಇತ್ಯಾದಿ.
ಈ ಟ್ಯುಟೋರಿಯಲ್ ನಲ್ಲಿ, ವಿವಿಧ ಅಲ್ಗಾರಿದಮ್ಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಪೈಥಾನ್ನಲ್ಲಿ ವಿಂಗಡಣೆಯು ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ನಾವು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುತ್ತೇವೆ.
ಪೈಥಾನ್ ವಿಂಗಡಣೆ

ಪೈಥಾನ್ ವಿಂಗಡಣೆಯ ಸಿಂಟ್ಯಾಕ್ಸ್
ವಿಂಗಡಣೆಯನ್ನು ನಿರ್ವಹಿಸಲು, ಪೈಥಾನ್ ಅಂತರ್ನಿರ್ಮಿತ ಕಾರ್ಯವನ್ನು ಒದಗಿಸುತ್ತದೆ ಅಂದರೆ "ವಿಂಗಡಣೆ()" ಕಾರ್ಯ. ಪಟ್ಟಿಯ ಡೇಟಾ ಅಂಶಗಳನ್ನು ಆರೋಹಣ ಕ್ರಮದಲ್ಲಿ ಅಥವಾ ಅವರೋಹಣ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಲು ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ಈ ಪರಿಕಲ್ಪನೆಯನ್ನು ಉದಾಹರಣೆಯೊಂದಿಗೆ ಅರ್ಥಮಾಡಿಕೊಳ್ಳೋಣ.
ಉದಾಹರಣೆ 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( “ List in ascending order: ”, a ) ```
ಔಟ್ಪುಟ್:

ಈ ಉದಾಹರಣೆಯಲ್ಲಿ, ನೀಡಲಾದ ಕ್ರಮಿಸದ ಪಟ್ಟಿಯನ್ನು “ವಿಂಗಡಣೆ( )” ಕಾರ್ಯವನ್ನು ಬಳಸಿಕೊಂಡು ಆರೋಹಣ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಲಾಗಿದೆ .
ಉದಾಹರಣೆ 2:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( “ List in descending order: ”, a ) ```
ಔಟ್ಪುಟ್

ಮೇಲಿನ ಉದಾಹರಣೆಯಲ್ಲಿ, ನೀಡಲಾದ ಅನಿಯಂತ್ರಿತ ಪಟ್ಟಿಯನ್ನು " sort( reverse = True ) " ಕಾರ್ಯವನ್ನು ಬಳಸಿಕೊಂಡು ಹಿಮ್ಮುಖ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಲಾಗಿದೆ.
ಸಮಯಸ್ಥಳ ಬಬಲ್ ವಿಂಗಡಣೆ O(n) O(n2) O(n2) O(1) ಹೌದು ಹೌದು ಅಳವಡಿಕೆ ವಿಂಗಡಣೆ O(n) O(n2) O(n2) O(1) ಹೌದು ಹೌದು ತ್ವರಿತ ವಿಂಗಡಣೆ O(n log(n)) O(n log(n)) O(n2) O(N) ಇಲ್ಲ ಹೌದು ವಿಲೀನಗೊಳಿಸಿ ವಿಂಗಡಿಸು O(n log(n)) O(n log(n)) O(n log(n)) O(N) ಹೌದು ಇಲ್ಲ ರಾಶಿ ವಿಂಗಡಣೆ O(n ಲಾಗ್ (n)) O(n log(n)) O(n log(n)) O(1) No ಹೌದು
ಮೇಲಿನ ಹೋಲಿಕೆ ಕೋಷ್ಟಕದಲ್ಲಿ “ O “ ದೊಡ್ಡ ಓಹ್ ಸಂಕೇತವಾಗಿದೆ ಆದರೆ “ n ” ಮತ್ತು “ N ” ಎಂದರೆ ಇನ್ಪುಟ್ನ ಗಾತ್ರ .
ಪದೇ ಪದೇ ಕೇಳಲಾಗುವ ಪ್ರಶ್ನೆಗಳು
Q #1) ಪೈಥಾನ್ನಲ್ಲಿ ವಿಂಗಡಣೆ () ಎಂದರೇನು?
ಉತ್ತರ: ಪೈಥಾನ್ನಲ್ಲಿ sort() ಎನ್ನುವುದು ಒಂದು ನಿರ್ದಿಷ್ಟ ಕ್ರಮದಲ್ಲಿ ಪಟ್ಟಿಗಳು ಅಥವಾ ಸರಣಿಗಳನ್ನು ವಿಂಗಡಿಸಲು ಬಳಸಲಾಗುವ ಒಂದು ಕಾರ್ಯವಾಗಿದೆ. ದೊಡ್ಡ ಯೋಜನೆಗಳಲ್ಲಿ ಕೆಲಸ ಮಾಡುವಾಗ ಈ ಕಾರ್ಯವು ವಿಂಗಡಿಸುವ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸುಲಭಗೊಳಿಸುತ್ತದೆ. ಡೆವಲಪರ್ಗಳಿಗೆ ಇದು ತುಂಬಾ ಸಹಾಯಕವಾಗಿದೆ.
Q #2) ನೀವು ಪೈಥಾನ್ನಲ್ಲಿ ಹೇಗೆ ವಿಂಗಡಿಸುತ್ತೀರಿ?
ಉತ್ತರ: ಪೈಥಾನ್ ಅಂಶವನ್ನು ವಿಂಗಡಿಸಲು ಬಳಸುವ ವಿವಿಧ ವಿಂಗಡಣೆ ತಂತ್ರಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ತ್ವರಿತ ವಿಂಗಡಣೆ, ವಿಲೀನ ವಿಂಗಡಣೆ, ಬಬಲ್ ವಿಂಗಡಣೆ, ಅಳವಡಿಕೆ ವಿಂಗಡಣೆ, ಇತ್ಯಾದಿ. ಎಲ್ಲಾ ವಿಂಗಡಣೆ ತಂತ್ರಗಳು ಸಮರ್ಥವಾಗಿರುತ್ತವೆ ಮತ್ತು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಸುಲಭವಾಗಿದೆ.
Q #3) ಪೈಥಾನ್ ಹೇಗೆ ಮಾಡುತ್ತದೆ ವಿಂಗಡಿಸು () ಕೆಲಸ?
ಉತ್ತರ: ವಿಂಗಡಣೆ()ಕಾರ್ಯವು ನೀಡಿದ ರಚನೆಯನ್ನು ಬಳಕೆದಾರರಿಂದ ಇನ್ಪುಟ್ ಆಗಿ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ವಿಂಗಡಿಸುವ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ನಿರ್ದಿಷ್ಟ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸುತ್ತದೆ. ಅಲ್ಗಾರಿದಮ್ನ ಆಯ್ಕೆಯು ಬಳಕೆದಾರರ ಆಯ್ಕೆಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಬಳಕೆದಾರರ ಅಗತ್ಯಗಳನ್ನು ಅವಲಂಬಿಸಿ ಬಳಕೆದಾರರು ತ್ವರಿತ ವಿಂಗಡಣೆ, ವಿಲೀನ ವಿಂಗಡಣೆ, ಬಬಲ್ ವಿಂಗಡಣೆ, ಅಳವಡಿಕೆ ವಿಂಗಡಣೆ, ಇತ್ಯಾದಿಗಳನ್ನು ಬಳಸಬಹುದು.
ತೀರ್ಮಾನ
ಮೇಲಿನ ಟ್ಯುಟೋರಿಯಲ್ ನಲ್ಲಿ, ನಾವು ಪೈಥಾನ್ನಲ್ಲಿ ವಿಂಗಡಣೆ ತಂತ್ರವನ್ನು ಚರ್ಚಿಸಿದ್ದೇವೆ ಸಾಮಾನ್ಯ ವಿಂಗಡಣೆಯ ತಂತ್ರಗಳು ಅನಾನುಕೂಲಗಳು. ನಾವು ಮೇಲಿನ ಎಲ್ಲಾ ತಂತ್ರಗಳನ್ನು ಸಹ ಹೋಲಿಸಿದ್ದೇವೆ.
ವಿಂಗಡಿಸುವ ಅಲ್ಗಾರಿದಮ್ಗಳ ಸಂಕೀರ್ಣತೆಸಮಯ ಸಂಕೀರ್ಣತೆಯು ನಿರ್ದಿಷ್ಟ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಚಲಾಯಿಸಲು ಕಂಪ್ಯೂಟರ್ ತೆಗೆದುಕೊಳ್ಳುವ ಸಮಯದ ಪ್ರಮಾಣವಾಗಿದೆ. ಇದು ಮೂರು ವಿಧದ ಸಮಯ ಸಂಕೀರ್ಣತೆಯ ಪ್ರಕರಣಗಳನ್ನು ಹೊಂದಿದೆ.
- ಕೆಟ್ಟ ಪ್ರಕರಣ: ಪ್ರೋಗ್ರಾಂ ಅನ್ನು ಚಲಾಯಿಸಲು ಕಂಪ್ಯೂಟರ್ ತೆಗೆದುಕೊಂಡ ಗರಿಷ್ಠ ಸಮಯ.
- ಸರಾಸರಿ ಪ್ರಕರಣ: ಪ್ರೋಗ್ರಾಂ ಅನ್ನು ಚಲಾಯಿಸಲು ಕಂಪ್ಯೂಟರ್ನಿಂದ ಕನಿಷ್ಠ ಮತ್ತು ಗರಿಷ್ಠ ಅವಧಿಯ ನಡುವೆ ತೆಗೆದುಕೊಂಡ ಸಮಯ.
- ಅತ್ಯುತ್ತಮ ಪ್ರಕರಣ: ಪ್ರೋಗ್ರಾಂ ಅನ್ನು ಚಲಾಯಿಸಲು ಕಂಪ್ಯೂಟರ್ ತೆಗೆದುಕೊಳ್ಳುವ ಕನಿಷ್ಠ ಸಮಯ. ಇದು ಸಮಯದ ಸಂಕೀರ್ಣತೆಯ ಅತ್ಯುತ್ತಮ ಪ್ರಕರಣವಾಗಿದೆ.
ಸಂಕೀರ್ಣತೆಯ ಸಂಕೇತಗಳು
ದೊಡ್ಡ ಓಹ್ ಸಂಕೇತ, O: ಬಿಗ್ ಓಹ್ ಸಂಕೇತವು ಮೇಲಿನ ಮಿತಿಯನ್ನು ತಿಳಿಸುವ ಅಧಿಕೃತ ಮಾರ್ಗವಾಗಿದೆ ಅಲ್ಗಾರಿದಮ್ಗಳ ಚಾಲನೆಯಲ್ಲಿರುವ ಸಮಯ. ಕೆಟ್ಟ ಸಮಯದ ಸಂಕೀರ್ಣತೆಯನ್ನು ಅಳೆಯಲು ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ ಅಥವಾ ಅಲ್ಗಾರಿದಮ್ ಪೂರ್ಣಗೊಳಿಸಲು ತೆಗೆದುಕೊಂಡ ದೊಡ್ಡ ಸಮಯವನ್ನು ನಾವು ಹೇಳುತ್ತೇವೆ.
ದೊಡ್ಡ ಒಮೆಗಾ ಸಂಕೇತ,  : ದೊಡ್ಡ ಒಮೆಗಾ ಸಂಕೇತ ಅಲ್ಗಾರಿದಮ್ಗಳ ಚಾಲನೆಯಲ್ಲಿರುವ ಸಮಯದ ಕಡಿಮೆ ಮಿತಿಯನ್ನು ತಿಳಿಸುವ ಅಧಿಕೃತ ಮಾರ್ಗ. ಅತ್ಯುತ್ತಮ ಸಂದರ್ಭದ ಸಮಯದ ಸಂಕೀರ್ಣತೆಯನ್ನು ಅಳೆಯಲು ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ ಅಥವಾ ಅಲ್ಗಾರಿದಮ್ ತೆಗೆದುಕೊಂಡ ಅತ್ಯುತ್ತಮ ಸಮಯವನ್ನು ನಾವು ಹೇಳುತ್ತೇವೆ.
: ದೊಡ್ಡ ಒಮೆಗಾ ಸಂಕೇತ ಅಲ್ಗಾರಿದಮ್ಗಳ ಚಾಲನೆಯಲ್ಲಿರುವ ಸಮಯದ ಕಡಿಮೆ ಮಿತಿಯನ್ನು ತಿಳಿಸುವ ಅಧಿಕೃತ ಮಾರ್ಗ. ಅತ್ಯುತ್ತಮ ಸಂದರ್ಭದ ಸಮಯದ ಸಂಕೀರ್ಣತೆಯನ್ನು ಅಳೆಯಲು ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ ಅಥವಾ ಅಲ್ಗಾರಿದಮ್ ತೆಗೆದುಕೊಂಡ ಅತ್ಯುತ್ತಮ ಸಮಯವನ್ನು ನಾವು ಹೇಳುತ್ತೇವೆ.
ಥೀಟಾ ಸಂಕೇತ, 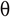 : ಥೀಟಾ ಸಂಕೇತವು ತಿಳಿಸಲು ಅಧಿಕೃತ ಮಾರ್ಗವಾಗಿದೆ ಎರಡೂ ಪರಿಮಿತಿಗಳು ಅಂದರೆ ಅಲ್ಗಾರಿದಮ್ ಪೂರ್ಣಗೊಳಿಸಲು ತೆಗೆದುಕೊಳ್ಳುವ ಸಮಯದ ಕಡಿಮೆ ಮತ್ತು ಮೇಲಿನದು.
: ಥೀಟಾ ಸಂಕೇತವು ತಿಳಿಸಲು ಅಧಿಕೃತ ಮಾರ್ಗವಾಗಿದೆ ಎರಡೂ ಪರಿಮಿತಿಗಳು ಅಂದರೆ ಅಲ್ಗಾರಿದಮ್ ಪೂರ್ಣಗೊಳಿಸಲು ತೆಗೆದುಕೊಳ್ಳುವ ಸಮಯದ ಕಡಿಮೆ ಮತ್ತು ಮೇಲಿನದು.
ಪೈಥಾನ್ನಲ್ಲಿ ವಿಂಗಡಣೆ ವಿಧಾನಗಳು
ಬಬಲ್ ವಿಂಗಡಣೆ
ಬಬಲ್ ವಿಂಗಡಣೆಯು ಡೇಟಾವನ್ನು ವಿಂಗಡಿಸಲು ಸರಳವಾದ ಮಾರ್ಗವಾಗಿದೆ ಇದು ಬ್ರೂಟ್ ಫೋರ್ಸ್ ತಂತ್ರವನ್ನು ಬಳಸುತ್ತದೆ. ಇದು ಪ್ರತಿ ಡೇಟಾ ಅಂಶಕ್ಕೆ ಪುನರಾವರ್ತನೆಯಾಗುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಹೋಲಿಸುತ್ತದೆವಿಂಗಡಿಸಲಾದ ಡೇಟಾವನ್ನು ಬಳಕೆದಾರರಿಗೆ ಒದಗಿಸಲು.
ಈ ತಂತ್ರವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ನಾವು ಒಂದು ಉದಾಹರಣೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ:
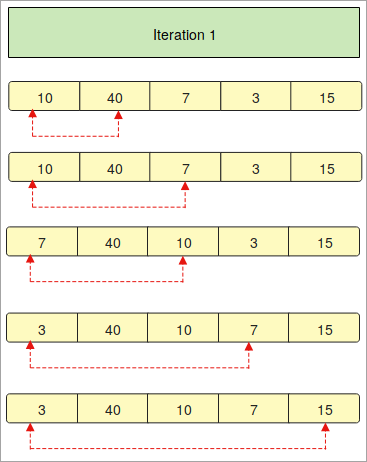
- ನಾವು ಅಂಶಗಳನ್ನು ಹೊಂದಿರುವ ಒಂದು ಶ್ರೇಣಿಯನ್ನು ಒದಗಿಸಿದ್ದೇವೆ “ 10, 40, 7, 3, 15 ”. ಈಗ, ಪೈಥಾನ್ನಲ್ಲಿನ ಬಬಲ್ ವಿಂಗಡಣೆ ತಂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ನಾವು ಈ ಶ್ರೇಣಿಯನ್ನು ಆರೋಹಣ ಕ್ರಮದಲ್ಲಿ ಜೋಡಿಸಬೇಕಾಗಿದೆ.
- ಅರೇಯನ್ನು ನಿರ್ದಿಷ್ಟ ಕ್ರಮದಲ್ಲಿ ಜೋಡಿಸುವುದು ಮೊದಲ ಹಂತವಾಗಿದೆ.
- “ ಪುನರಾವರ್ತನೆ 1 ” ನಲ್ಲಿ, ನಾವು ಸರಣಿಯ ಮೊದಲ ಅಂಶವನ್ನು ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಒಂದೊಂದಾಗಿ ಹೋಲಿಸುತ್ತಿದ್ದೇವೆ.
- ಕೆಂಪು ಬಾಣಗಳು ರಚನೆಯ ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಮೊದಲ ಅಂಶಗಳ ಹೋಲಿಕೆಯನ್ನು ವಿವರಿಸುತ್ತದೆ.
- ನೀವು "10" ಅನ್ನು "40" ಗಿಂತ ಚಿಕ್ಕದಾಗಿದೆ ಎಂದು ಗಮನಿಸಿದರೆ, ಅದು ಒಂದೇ ಆಗಿರುತ್ತದೆ ಇರಿಸಿ ಆದರೆ ಮುಂದಿನ ಅಂಶ " 7 " " 10 " ಗಿಂತ ಚಿಕ್ಕದಾಗಿದೆ. ಆದ್ದರಿಂದ ಅದನ್ನು ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಮೊದಲ ಸ್ಥಾನಕ್ಕೆ ಬರುತ್ತದೆ.
- ಮೂಲಕಗಳನ್ನು ವಿಂಗಡಿಸಲು ಮೇಲಿನ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಮತ್ತೆ ಮತ್ತೆ ನಿರ್ವಹಿಸಲಾಗುತ್ತದೆ.
 3>
3>
-
- “ ಪುನರಾವರ್ತನೆ 2 ” ರಲ್ಲಿ ಎರಡನೇ ಅಂಶವು ರಚನೆಯ ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಹೋಲಿಸುತ್ತದೆ.
- ಹೋಲಿಸಲಾದ ಅಂಶವು ಚಿಕ್ಕದಾಗಿದ್ದರೆ, ಅದು ಬದಲಾಯಿಸಿಕೊಳ್ಳಿ, ಇಲ್ಲದಿದ್ದರೆ ಅದು ಅದೇ ಸ್ಥಳದಲ್ಲಿ ಉಳಿಯುತ್ತದೆ ರಚನೆಯ ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಮೂರನೇ ಅಂಶವನ್ನು ಹೋಲಿಸಲಾಗುತ್ತದೆ. " ಪುನರಾವರ್ತನೆ 4 " ಎರಡನೇ ಕೊನೆಯ ಅಂಶವನ್ನು ರಚನೆಯ ಇತರ ಅಂಶಗಳೊಂದಿಗೆ ಹೋಲಿಸಲಾಗುತ್ತದೆ.
- ಇನ್ಈ ಹಂತವನ್ನು ಆರೋಹಣ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಲಾಗಿದೆ.

ಬಬಲ್ ವಿಂಗಡಣೆಗಾಗಿ ಪ್ರೋಗ್ರಾಂ
``` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Unsorted List: ", unsorted_list) print("Sorted List using Bubble Sort Technique: ", Bubble_Sort(unsorted_list)) ``` ಔಟ್ಪುಟ್

ಬಬಲ್ ವಿಧದ ಸಮಯ ಸಂಕೀರ್ಣತೆ
- ಕೆಟ್ಟ ಪ್ರಕರಣ: ಬಬಲ್ ವಿಂಗಡಣೆಗೆ ಕೆಟ್ಟ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n 2).
- ಸರಾಸರಿ ಪ್ರಕರಣ: ಬಬಲ್ ವಿಂಗಡಣೆಗೆ ಸರಾಸರಿ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n 2).
- ಅತ್ಯುತ್ತಮ ಪ್ರಕರಣ: ಬಬಲ್ ವಿಂಗಡಣೆಗೆ ಉತ್ತಮ ಸಮಯ ಸಂಕೀರ್ಣತೆ O(n).
ಅನುಕೂಲಗಳು
- ಇದನ್ನು ಹೆಚ್ಚಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ ಮತ್ತು ಕಾರ್ಯಗತಗೊಳಿಸಲು ಸುಲಭವಾಗಿದೆ.
- ಅಲ್ಪಾವಧಿಯ ಸಂಗ್ರಹಣೆಯ ಬಳಕೆಯಿಲ್ಲದೆ ನಾವು ಡೇಟಾ ಅಂಶಗಳನ್ನು ವಿನಿಮಯ ಮಾಡಿಕೊಳ್ಳಬಹುದು.
- ಇದಕ್ಕೆ ಕಡಿಮೆ ಅಗತ್ಯವಿದೆ ಸ್ಪೇಸ್.
ಅನುಕೂಲಗಳು
- ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ದೊಡ್ಡ ಡೇಟಾ ಅಂಶಗಳೊಂದಿಗೆ ವ್ಯವಹರಿಸುವಾಗ ಇದು ಉತ್ತಮವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸಲಿಲ್ಲ.
- ಇದು ಪ್ರತಿ "n" ಸಂಖ್ಯೆಯ ಡೇಟಾ ಅಂಶಗಳಿಗೆ ವಿಂಗಡಿಸಲು n 2 ಹಂತಗಳ ಅಗತ್ಯವಿದೆ.
- ನೈಜ-ಪ್ರಪಂಚದ ಅಪ್ಲಿಕೇಶನ್ಗಳಿಗೆ ಇದು ನಿಜವಾಗಿಯೂ ಉತ್ತಮವಾಗಿಲ್ಲ.
ಅಳವಡಿಕೆ ವಿಂಗಡಿಸಿ
ಇನ್ಸರ್ಶನ್ ವಿಂಗಡಣೆಯು ಒಂದು ಸುಲಭ ಮತ್ತು ಸರಳವಾದ ವಿಂಗಡಣೆಯ ತಂತ್ರವಾಗಿದ್ದು ಅದು ಪ್ಲೇಯಿಂಗ್ ಕಾರ್ಡ್ಗಳನ್ನು ವಿಂಗಡಿಸುವಂತೆಯೇ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ. ಅಳವಡಿಕೆಯ ವಿಂಗಡಣೆಯು ಪ್ರತಿಯೊಂದು ಅಂಶವನ್ನು ಒಂದೊಂದಾಗಿ ಇನ್ನೊಂದಕ್ಕೆ ಹೋಲಿಸುವ ಮೂಲಕ ಅಂಶಗಳನ್ನು ವಿಂಗಡಿಸುತ್ತದೆ. ಅಂಶವು ಇತರಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿದ್ದರೆ ಅಥವಾ ಚಿಕ್ಕದಾಗಿದ್ದರೆ ಅಂಶಗಳನ್ನು ಆಯ್ಕೆಮಾಡಲಾಗುತ್ತದೆ ಮತ್ತು ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ " 100, 50, 30, 40, 10 " ಅಂಶಗಳನ್ನು ಹೊಂದಿರುವ ಒಂದು ಶ್ರೇಣಿ.

ಅಳವಡಿಕೆಯ ವಿಂಗಡಣೆಗಾಗಿ ಪ್ರೋಗ್ರಾಂ
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j >= 0 and key_value array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("The unsorted array: ", array) InsertionSort(array) print ("The sorted array using the Insertion Sort: ") for i in range(len(array)): print (array[i]) ``` ಔಟ್ಪುಟ್
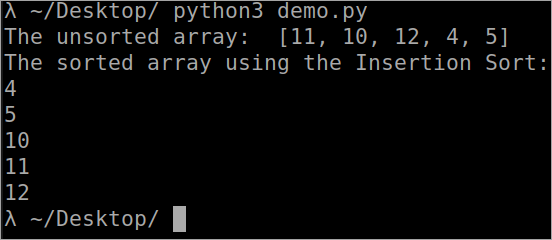
ಅಳವಡಿಕೆ ವಿಧದ ಸಮಯದ ಸಂಕೀರ್ಣತೆ
- ಕೆಟ್ಟ ಪ್ರಕರಣ: ಅಳವಡಿಕೆಯ ವಿಂಗಡಣೆಗೆ ಕೆಟ್ಟ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n 2).
- ಸರಾಸರಿ ಪ್ರಕರಣ: ಅಳವಡಿಕೆಯ ವಿಂಗಡಣೆಗೆ ಸರಾಸರಿ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n 2) ಆಗಿದೆ.
- ಅತ್ಯುತ್ತಮ ಪ್ರಕರಣ: ಒಳಸೇರಿಸುವಿಕೆಯ ವಿಂಗಡಣೆಗೆ ಉತ್ತಮ ಸಮಯ ಸಂಕೀರ್ಣತೆ O(n).
ಅನುಕೂಲಗಳು
- ಇದು ಸರಳವಾಗಿದೆ. ಮತ್ತು ಕಾರ್ಯಗತಗೊಳಿಸಲು ಸುಲಭವಾಗಿದೆ.
- ಕಡಿಮೆ ಸಂಖ್ಯೆಯ ಡೇಟಾ ಅಂಶಗಳೊಂದಿಗೆ ವ್ಯವಹರಿಸುವಾಗ ಇದು ಉತ್ತಮವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.
- ಇದರ ಅನುಷ್ಠಾನಕ್ಕೆ ಹೆಚ್ಚಿನ ಸ್ಥಳಾವಕಾಶದ ಅಗತ್ಯವಿಲ್ಲ.
ಅನನುಕೂಲಗಳು
- ಅಪಾರ ಸಂಖ್ಯೆಯ ಡೇಟಾ ಅಂಶಗಳನ್ನು ವಿಂಗಡಿಸಲು ಇದು ಸಹಾಯಕವಾಗುವುದಿಲ್ಲ.
- ಇತರ ವಿಂಗಡಣೆ ತಂತ್ರಗಳಿಗೆ ಹೋಲಿಸಿದರೆ ಅದು ಉತ್ತಮವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವುದಿಲ್ಲ.
ವಿಲೀನ ವಿಂಗಡಣೆ
ಈ ವಿಂಗಡಣೆ ವಿಧಾನವು ಅಂಶಗಳನ್ನು ನಿರ್ದಿಷ್ಟ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಲು ಡಿವೈಡ್ ಮತ್ತು ಕಾಂಕರ್ ವಿಧಾನವನ್ನು ಬಳಸುತ್ತದೆ. ವಿಲೀನ ವಿಂಗಡಣೆಯ ಸಹಾಯದಿಂದ ವಿಂಗಡಿಸುವಾಗ, ದಿಅಂಶಗಳನ್ನು ಅರ್ಧ ಭಾಗಗಳಾಗಿ ವಿಂಗಡಿಸಲಾಗಿದೆ ಮತ್ತು ನಂತರ ಅವುಗಳನ್ನು ವಿಂಗಡಿಸಲಾಗುತ್ತದೆ. ಎಲ್ಲಾ ಭಾಗಗಳನ್ನು ವಿಂಗಡಿಸಿದ ನಂತರ, ಮತ್ತೆ ಅಂಶಗಳು ಒಂದು ಪರಿಪೂರ್ಣ ಕ್ರಮವನ್ನು ರೂಪಿಸಲು ಸೇರಿಕೊಳ್ಳುತ್ತವೆ.
ಈ ತಂತ್ರವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಒಂದು ಉದಾಹರಣೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ
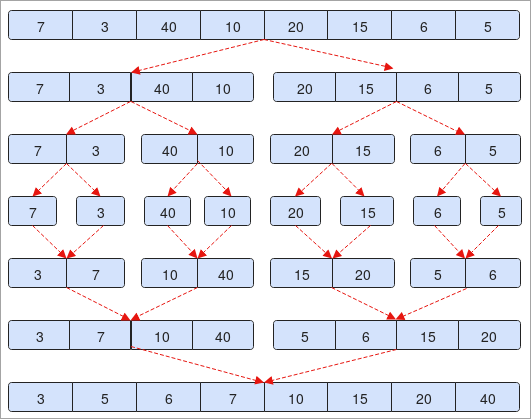
- ನಮಗೆ ಒದಗಿಸಲಾಗಿದೆ ಒಂದು ಶ್ರೇಣಿ "7, 3, 40, 10, 20, 15, 6, 5". ರಚನೆಯು 7 ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ನಾವು ಅದನ್ನು ಅರ್ಧಕ್ಕೆ ವಿಭಜಿಸಿದರೆ ( 0 + 7 / 2 = 3 ).
- ಎರಡನೆಯ ಹಂತದಲ್ಲಿ, ಅಂಶಗಳನ್ನು ಎರಡು ಭಾಗಗಳಾಗಿ ವಿಂಗಡಿಸಲಾಗಿದೆ ಎಂದು ನೀವು ನೋಡುತ್ತೀರಿ. ಪ್ರತಿಯೊಂದೂ ಅದರಲ್ಲಿ 4 ಅಂಶಗಳನ್ನು ಹೊಂದಿದೆ.
- ಇದಲ್ಲದೆ, ಅಂಶಗಳನ್ನು ಮತ್ತೆ ವಿಂಗಡಿಸಲಾಗಿದೆ ಮತ್ತು ಪ್ರತಿಯೊಂದೂ 2 ಅಂಶಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.
- ಒಂದು ರಚನೆಯಲ್ಲಿ ಕೇವಲ ಒಂದು ಅಂಶ ಮಾತ್ರ ಇರುವವರೆಗೆ ಈ ಪ್ರಕ್ರಿಯೆಯು ಮುಂದುವರಿಯುತ್ತದೆ. ಹಂತ ಸಂಖ್ಯೆ ನೋಡಿ. ಚಿತ್ರದಲ್ಲಿ 4.
- ಈಗ, ನಾವು ಅಂಶಗಳನ್ನು ವಿಂಗಡಿಸುತ್ತೇವೆ ಮತ್ತು ವಿಭಜಿಸಿದಂತೆ ಅವುಗಳನ್ನು ಸೇರಲು ಪ್ರಾರಂಭಿಸುತ್ತೇವೆ.
- ಹಂತ ಸಂಖ್ಯೆ. 5 3 ಕ್ಕಿಂತ 7 ದೊಡ್ಡದಾಗಿದೆ ಎಂದು ನೀವು ಗಮನಿಸಿದರೆ, ಆದ್ದರಿಂದ ನಾವು ಅವುಗಳನ್ನು ವಿನಿಮಯ ಮಾಡಿಕೊಳ್ಳುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು ಮುಂದಿನ ಹಂತದಲ್ಲಿ ಮತ್ತು ಪ್ರತಿಯಾಗಿ ಸೇರಿಸುತ್ತೇವೆ.
- ಕೊನೆಯಲ್ಲಿ, ನಮ್ಮ ರಚನೆಯು ಆರೋಹಣ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಲ್ಪಡುತ್ತಿರುವುದನ್ನು ನೀವು ಗಮನಿಸಬಹುದು.
ವಿಲೀನ ವಿಂಗಡಣೆಗಾಗಿ ಪ್ರೋಗ್ರಾಂ
``` def MergeSort(arr): if len(arr) > 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i len(L) and j len(R): if L[i] R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i len(L): arr[k] = L[i] i += 1 k += 1 while j len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i in range(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Given array is", end="\n") PrintSortedList(arr) MergeSort(arr) print("Sorted array is: ", end="\n") PrintSortedList(arr) ``` ಔಟ್ಪುಟ್
ವಿಲೀನ ವಿಧದ ಸಮಯದ ಸಂಕೀರ್ಣತೆ
- ಕೆಟ್ಟ ಪ್ರಕರಣ: ವಿಲೀನ ವಿಂಗಡಣೆಗೆ ಕೆಟ್ಟ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n ಲಾಗ್( n )).
- ಸರಾಸರಿ ಪ್ರಕರಣ: ವಿಲೀನ ವಿಂಗಡಣೆಯ ಸರಾಸರಿ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n ಲಾಗ್( n )).
- ಅತ್ಯುತ್ತಮ ಪ್ರಕರಣ: ವಿಲೀನ ವಿಂಗಡಣೆಗೆ ಉತ್ತಮ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n log( n )).
ಅನುಕೂಲಗಳು
- ಈ ವಿಂಗಡಣೆ ತಂತ್ರಕ್ಕೆ ಫೈಲ್ ಗಾತ್ರವು ಅಪ್ರಸ್ತುತವಾಗುತ್ತದೆ.
- ಸಾಮಾನ್ಯವಾಗಿ ಅನುಕ್ರಮ ಕ್ರಮದಲ್ಲಿ ಪ್ರವೇಶಿಸುವ ಡೇಟಾಗೆ ಈ ತಂತ್ರವು ಉತ್ತಮವಾಗಿದೆ. ಉದಾಹರಣೆಗೆ, ಲಿಂಕ್ ಮಾಡಿದ ಪಟ್ಟಿಗಳು, ಟೇಪ್ ಡ್ರೈವ್, ಇತ್ಯಾದಿ.
ಅನುಕೂಲಗಳು
- ಇತರರಿಗೆ ಹೋಲಿಸಿದರೆ ಇದಕ್ಕೆ ಹೆಚ್ಚಿನ ಸ್ಥಳಾವಕಾಶ ಬೇಕಾಗುತ್ತದೆ ವಿಂಗಡಣೆ ತಂತ್ರಗಳು.
- ಇದು ಇತರರಿಗಿಂತ ತುಲನಾತ್ಮಕವಾಗಿ ಕಡಿಮೆ ದಕ್ಷವಾಗಿದೆ.
ತ್ವರಿತ ವಿಂಗಡಣೆ
ಶೀಘ್ರ ವಿಂಗಡಣೆ ಮತ್ತೊಮ್ಮೆ ಪಟ್ಟಿಯ ಅಂಶಗಳನ್ನು ವಿಂಗಡಿಸಲು ವಿಭಜಿಸಿ ಮತ್ತು ವಶಪಡಿಸಿಕೊಳ್ಳುವ ವಿಧಾನವನ್ನು ಬಳಸುತ್ತದೆ ಅಥವಾ ಒಂದು ಶ್ರೇಣಿ. ಇದು ಪಿವೋಟ್ ಅಂಶಗಳನ್ನು ಗುರಿಯಾಗಿಸುತ್ತದೆ ಮತ್ತು ಆಯ್ದ ಪಿವೋಟ್ ಅಂಶದ ಪ್ರಕಾರ ಅಂಶಗಳನ್ನು ವಿಂಗಡಿಸುತ್ತದೆ.
ಉದಾಹರಣೆಗೆ
- ನಮಗೆ ಮೂಲಾಂಶಗಳನ್ನು ಹೊಂದಿರುವ ರಚನೆಯನ್ನು ಒದಗಿಸಲಾಗಿದೆ “ 1 ,8,3,9,4,5,7 ”.
- ನಾವು “7” ಅನ್ನು ಪೈಲಟ್ ಅಂಶ ಎಂದು ಭಾವಿಸೋಣ.
- ಈಗ ನಾವು ಶ್ರೇಣಿಯನ್ನು ವಿಭಜಿಸುತ್ತೇವೆ ಎಡಭಾಗವು ಪಿವೋಟ್ ಅಂಶ " 7 " ಗಿಂತ ಚಿಕ್ಕದಾಗಿರುವ ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿದೆ ಮತ್ತು ಬಲಭಾಗವು ಪಿವೋಟ್ ಅಂಶ " 7 " ಗಿಂತ ಹೆಚ್ಚಿನ ಅಂಶಗಳನ್ನು ಒಳಗೊಂಡಿದೆ.
- ನಾವು ಈಗ ಎರಡು ಅರೇಗಳನ್ನು ಹೊಂದಿದ್ದೇವೆ " 1,3,4,5 ” ಮತ್ತು “ 8, 9 ”.
- ಮತ್ತೆ, ನಾವು ಮೇಲೆ ಮಾಡಿದಂತೆಯೇ ಎರಡೂ ಅರೇಗಳನ್ನು ವಿಭಜಿಸಬೇಕು. ಒಂದೇ ವ್ಯತ್ಯಾಸವೆಂದರೆ ಪಿವೋಟ್ ಅಂಶಗಳು ಬದಲಾಗುತ್ತವೆ.
- ನಾವು ಸರಣಿಯಲ್ಲಿ ಏಕ ಅಂಶವನ್ನು ಪಡೆಯುವವರೆಗೆ ನಾವು ಸರಣಿಗಳನ್ನು ವಿಭಜಿಸಬೇಕಾಗಿದೆ.
- ಕೊನೆಯಲ್ಲಿ, a ನಲ್ಲಿ ಎಲ್ಲಾ ಪಿವೋಟ್ ಅಂಶಗಳನ್ನು ಸಂಗ್ರಹಿಸಿ ಎಡದಿಂದ ಬಲಕ್ಕೆ ಅನುಕ್ರಮ ಮತ್ತು ನೀವು ವಿಂಗಡಿಸಲಾಗುತ್ತದೆ ಪಡೆಯುತ್ತೀರಿರಚನೆ
ತ್ವರಿತ ವಿಂಗಡಣೆಯ ಸಮಯದ ಸಂಕೀರ್ಣತೆ
- ಕೆಟ್ಟ ಪ್ರಕರಣ: ತ್ವರಿತ ವಿಂಗಡಣೆಗೆ ಕೆಟ್ಟ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n 2).
- ಸರಾಸರಿ ಪ್ರಕರಣ: ತ್ವರಿತ ವಿಂಗಡಣೆಗೆ ಸರಾಸರಿ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n log( n ) ).
- ಅತ್ಯುತ್ತಮ ಪ್ರಕರಣ: ತ್ವರಿತ ವಿಂಗಡಣೆಗೆ ಉತ್ತಮ ಸಮಯ ಸಂಕೀರ್ಣತೆ ಎಂದರೆ O( n log( n )). 16>
- ಇದು ಪೈಥಾನ್ನಲ್ಲಿ ಅತ್ಯುತ್ತಮ ವಿಂಗಡಣೆ ಅಲ್ಗಾರಿದಮ್ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ.
- ದೊಡ್ಡ ಪ್ರಮಾಣದ ಡೇಟಾವನ್ನು ನಿರ್ವಹಿಸುವಾಗ ಇದು ಉಪಯುಕ್ತವಾಗಿದೆ.
- ಇದಕ್ಕೆ ಹೆಚ್ಚುವರಿ ಸ್ಥಳಾವಕಾಶದ ಅವಶ್ಯಕತೆ ಇಲ್ಲ ಅಳವಡಿಕೆಯ ವಿಂಗಡಣೆ.
- ನಾವು ಈಗಾಗಲೇ ವಿಂಗಡಿಸಲಾದ ಪಟ್ಟಿಯನ್ನು ಹೊಂದಿರುವಾಗ ಈ ವಿಂಗಡಣೆ ವಿಧಾನವು ಉಪಯುಕ್ತವಲ್ಲ.
- ನಮಗೆ “ 40, 100, 30, 50, 10 ” ಅಂಶಗಳನ್ನು ಹೊಂದಿರುವ ಒಂದು ಶ್ರೇಣಿಯನ್ನು ಒದಗಿಸಲಾಗಿದೆ.
- “ ಹಂತ 1 ” ನಲ್ಲಿ ನಾವು ಅದರ ಪ್ರಕಾರ ಮರವನ್ನು ಮಾಡಿದ್ದೇವೆ ರಚನೆಯಲ್ಲಿನ ಅಂಶಗಳ ಉಪಸ್ಥಿತಿ ಅವರೋಹಣ ಕ್ರಮದಲ್ಲಿ ಅಂಶಗಳು. ಮಹಾನ್ ಅಂಶ ತಿನ್ನುವೆಮೇಲ್ಭಾಗದಲ್ಲಿ (ಮೂಲ) ಮತ್ತು ಚಿಕ್ಕ ಅಂಶವು ಕೆಳಭಾಗದಲ್ಲಿ (ಲೀಫ್ ನೋಡ್ಗಳು) ನೆಲೆಸಿದೆ. ನೀಡಲಾದ ರಚನೆಯು “ 100, 50, 30, 40, 10 ” ಆಗುತ್ತದೆ.
ಅನುಕೂಲಗಳು
ಹೀಪ್ ವಿಂಗಡಣೆ
ಹೀಪ್ ವಿಂಗಡಣೆಯು ಬೈನರಿ ಸರ್ಚ್ ಟ್ರೀಯ ಸುಧಾರಿತ ಆವೃತ್ತಿಯಾಗಿದೆ. . ರಾಶಿ ವಿಂಗಡಣೆಯಲ್ಲಿ, ಲೀಫ್ ನೋಡ್ಗಳೊಂದಿಗೆ ಬೇರಿನೊಂದಿಗೆ ಹೋಲಿಸಿದಾಗ, ರಚನೆಯ ಶ್ರೇಷ್ಠ ಅಂಶವನ್ನು ಯಾವಾಗಲೂ ಮತ್ತು ನಂತರ ಮರದ ಮೂಲದ ಮೇಲೆ ಇರಿಸಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆಗೆ:
13> 
- “ ಹಂತ 3 ” ರಲ್ಲಿ, ನಾವು ಕನಿಷ್ಠ ರಾಶಿಯನ್ನು ಮಾಡುವುದರಿಂದ ನಾವು ರಚನೆಯ ಕನಿಷ್ಠ ಅಂಶಗಳನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು. ಇದನ್ನು ಮಾಡುವುದರಿಂದ, ನಾವು ಗರಿಷ್ಠ ಮತ್ತು ಕನಿಷ್ಠ ಅಂಶಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ.

- “ ಹಂತ 4 ” ನಲ್ಲಿ ಅದೇ ಹಂತಗಳನ್ನು ನಿರ್ವಹಿಸುವ ಮೂಲಕ ನಾವು ವಿಂಗಡಿಸಲಾದ ಶ್ರೇಣಿಯನ್ನು ಪಡೆಯುತ್ತೇವೆ.

ಹೀಪ್ ವಿಂಗಡಣೆಗಾಗಿ ಪ್ರೋಗ್ರಾಂ
``` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left n and arr[ larger_element ] arr[ left ]: larger_element = left if right n and arr[ larger_element ] arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ] HeapSortify( arr, n, larger_element ) def HeapSort( arr ): n = len( arr ) for i in range( n//2 - 1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " The unsorted array is: ", arr ) HeapSort( arr ) n = len( arr ) print( " The sorted array sorted by the Heap Sort: " ) for i in range( n ): print( arr[ i ] ) ```
ಔಟ್ಪುಟ್
ಹೀಪ್ ವಿಂಗಡಣೆಯ ಸಮಯದ ಸಂಕೀರ್ಣತೆ
- ಕೆಟ್ಟ ಪ್ರಕರಣ: ಹೀಪ್ ವಿಂಗಡಣೆಯ ಕೆಟ್ಟ ಸಮಯದ ಸಂಕೀರ್ಣತೆ O( n log( n )).
- ಸರಾಸರಿ ಪ್ರಕರಣ: ಹೀಪ್ ವಿಂಗಡಣೆಗೆ ಸರಾಸರಿ ಸಮಯ ಸಂಕೀರ್ಣತೆ O( n ಲಾಗ್( n )).
- ಉತ್ತಮ ಪ್ರಕರಣ: ಹೀಪ್ ವಿಂಗಡಣೆಗೆ ಉತ್ತಮ ಸಮಯ ಸಂಕೀರ್ಣತೆ isO( n log( n )).
ಅನುಕೂಲಗಳು
- ಅದರ ಉತ್ಪಾದಕತೆಯಿಂದಾಗಿ ಇದನ್ನು ಹೆಚ್ಚಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ.
- ಇದು ಮಾಡಬಹುದು ಇನ್-ಪ್ಲೇಸ್ ಅಲ್ಗಾರಿದಮ್ ಆಗಿ ಅಳವಡಿಸಲಾಗಿದೆ.
- ಇದಕ್ಕೆ ದೊಡ್ಡ ಸಂಗ್ರಹಣೆಯ ಅಗತ್ಯವಿರುವುದಿಲ್ಲ.
ಅನುಕೂಲಗಳು
- ಇದಕ್ಕೆ ಸ್ಥಳಾವಕಾಶದ ಅಗತ್ಯವಿದೆ ಅಂಶಗಳನ್ನು ವಿಂಗಡಿಸುವುದು.
- ಇದು ಅಂಶಗಳ ವಿಂಗಡಣೆಗಾಗಿ ಮರವನ್ನು ಮಾಡುತ್ತದೆ.
ವಿಂಗಡಣೆ ತಂತ್ರಗಳ ನಡುವಿನ ಹೋಲಿಕೆ
| ವಿಂಗಡಿಸುವ ವಿಧಾನ | ಅತ್ಯುತ್ತಮ ಸಂದರ್ಭದ ಸಮಯದ ಸಂಕೀರ್ಣತೆ | ಸರಾಸರಿ ಪ್ರಕರಣದ ಸಮಯದ ಸಂಕೀರ್ಣತೆ | ಕೆಟ್ಟ ಸಂದರ್ಭದಲ್ಲಿ ಸಮಯ ಸಂಕೀರ್ಣತೆ | ಸ್ಪೇಸ್ ಸಂಕೀರ್ಣತೆ | ಸ್ಥಿರತೆ | ಇನ್ - |
|---|