ისწავლეთ როგორ გამოიყენოთ Python Sort ფუნქცია სიების, მასივების, ლექსიკონების და ა.შ დასალაგებლად Python-ში დახარისხების სხვადასხვა მეთოდებისა და ალგორითმების გამოყენებით:
სორტირება არის ტექნიკა, რომელიც გამოიყენება დახარისხებისთვის მონაცემები თანმიმდევრული თანმიმდევრობით, როგორც ზრდადი, ისე კლებადი თანმიმდევრობით.
ხშირად დიდი პროექტების მონაცემები არ არის დალაგებული სწორი თანმიმდევრობით და ეს ქმნის პრობლემებს საჭირო მონაცემების ეფექტურად წვდომისა და მიღებისას.
ამ პრობლემის გადასაჭრელად გამოიყენება დახარისხების ტექნიკა. Python გთავაზობთ სხვადასხვა დახარისხების ტექნიკას მაგალითად, Bubble sort, Insertion sort, Merge sort, Quicksort და ა.შ.
ამ სახელმძღვანელოში ჩვენ გავიგებთ როგორ მუშაობს პითონში დახარისხება სხვადასხვა ალგორითმების გამოყენებით.
Python სორტირება

Python სორტირების სინტაქსი
დახარისხების შესასრულებლად, Python უზრუნველყოფს ჩაშენებულ ფუნქციას, ანუ " sort() " ფუნქციას. იგი გამოიყენება სიის მონაცემთა ელემენტების ზრდის ან კლების მიხედვით დასალაგებლად.
მოდით, გავიგოთ ეს კონცეფცია მაგალითით.
მაგალითი 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( “ List in ascending order: ”, a ) ```
გამომავალი:

ამ მაგალითში მოცემული დაურიგებელი სია დალაგებულია ზრდადი თანმიმდევრობით " sort( ) " ფუნქციის გამოყენებით. .
მაგალითი 2:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( “ List in descending order: ”, a ) ```
გამომავალი

ზემოთ მაგალითში, მოცემული დაურიგებელი სია დალაგებულია საპირისპირო თანმიმდევრობით ფუნქციის „ sort( reverse = True )“ გამოყენებით.
დროადგილი ბუშტის დალაგება O(n) O(n2) O(n2) O(1) დიახ დიახ ჩასმის დალაგება O(n) O(n2) O(n2) O(1) დიახ დიახ სწრაფი დახარისხება O(n log(n)) O(n log(n)) O(n2) O(N) არა დიახ შერწყმა დალაგება O(n log(n)) O(n log(n)) O(n log(n)) O(N) დიახ არა გროვების დალაგება O(n ჟურნალი (n)) O(n log(n)) O(n log(n)) O(1) არა დიახ
ზემოთ შედარების ცხრილში "O" არის ზემოთ აღწერილი დიდი Oh აღნიშვნა, ხოლო "n" და "N" ნიშნავს შეყვანის ზომას. .
ხშირად დასმული კითხვები
Q #1) რა არის დალაგება () Python-ში?
პასუხი: Python-ში sort() არის ფუნქცია, რომელიც გამოიყენება სიების ან მასივების კონკრეტული თანმიმდევრობით დასალაგებლად. ეს ფუნქცია აადვილებს დახარისხების პროცესს დიდ პროექტებზე მუშაობისას. ეს ძალიან სასარგებლოა დეველოპერებისთვის.
Q #2) როგორ ახარისხებთ Python-ში?
პასუხი: Python გთავაზობთ სხვადასხვა დახარისხების ტექნიკას, რომლებიც გამოიყენება ელემენტის დასალაგებლად. მაგალითად, სწრაფი დალაგება, შერწყმა დახარისხება, ბუშტების დალაგება, ჩასმა და ა.შ. დალაგების ყველა ტექნიკა ეფექტური და ადვილად გასაგებია.
Q #3) როგორ მუშაობს Python დახარისხება () სამუშაო?
პასუხი: დალაგება()ფუნქცია იღებს მოცემულ მასივს, როგორც შეყვანა მომხმარებლისგან და ახარისხებს მას კონკრეტული თანმიმდევრობით დახარისხების ალგორითმის გამოყენებით. ალგორითმის შერჩევა დამოკიდებულია მომხმარებლის არჩევანზე. მომხმარებლებს შეუძლიათ გამოიყენონ სწრაფი დალაგება, შერწყმა დახარისხება, ბუშტუკების დალაგება, ჩასმა და ა.შ. მომხმარებლის საჭიროებიდან გამომდინარე.
დასკვნა
ზემოთ ინსტრუქციაში, ჩვენ განვიხილეთ დალაგების ტექნიკა Python-ში. ზოგადი დახარისხების ტექნიკა.
- ბუშტუკების დალაგება
- ჩასმა დახარისხება
- სწრაფი დახარისხება
ვისწავლეთ მათი დროის სირთულეები და უპირატესობები & ნაკლოვანებები. ჩვენ ასევე შევადარეთ ყველა ზემოთ ჩამოთვლილი ტექნიკა.
დახარისხების ალგორითმების სირთულედროის სირთულე არის დრო, რომელიც კომპიუტერს სჭირდება კონკრეტული ალგორითმის გასაშვებად. მას აქვს სამი სახის დროის სირთულის შემთხვევები.
- უარესი შემთხვევა: პროგრამის გაშვებას კომპიუტერის მაქსიმალური დრო სჭირდება.
- საშუალო შემთხვევა: კომპიუტერის მიერ პროგრამის გასაშვებად მინიმალურ და მაქსიმუმს შორის გატარებული დრო.
- საუკეთესო შემთხვევა: მინიმალური დრო, რომელიც კომპიუტერს სჭირდება პროგრამის გასაშვებად. ეს არის დროის სირთულის საუკეთესო შემთხვევა.
სირთულის აღნიშვნები
Big Oh ნოტაცია, O: Big oh ნოტაცია არის ოფიციალური გზა ზედა ზღვარის გადმოსაცემად ალგორითმების მუშაობის დროის შესახებ. იგი გამოიყენება უარეს შემთხვევაში დროის სირთულის გასაზომად ან ჩვენ ვამბობთ, რომ ალგორითმის მიერ დასრულებული დროის უდიდესი რაოდენობაა.
დიდი ომეგა ნოტაცია,  : დიდი ომეგა აღნიშვნა არის ოფიციალური გზა ალგორითმების მუშაობის დროის ყველაზე დაბალი ზღვრის გადმოსაცემად. იგი გამოიყენება საუკეთესო შემთხვევის დროის სირთულის გასაზომად ან ჩვენ ვამბობთ ალგორითმის მიერ დახარჯული დროის შესანიშნავ რაოდენობას.
: დიდი ომეგა აღნიშვნა არის ოფიციალური გზა ალგორითმების მუშაობის დროის ყველაზე დაბალი ზღვრის გადმოსაცემად. იგი გამოიყენება საუკეთესო შემთხვევის დროის სირთულის გასაზომად ან ჩვენ ვამბობთ ალგორითმის მიერ დახარჯული დროის შესანიშნავ რაოდენობას.
თეტა ნოტაცია, 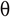 : თეტა ნოტაცია არის გადაცემის ოფიციალური გზა. ორივე საზღვრები, ანუ ალგორითმის დასრულებისთვის საჭირო დროის ქვედა და ზედა.
: თეტა ნოტაცია არის გადაცემის ოფიციალური გზა. ორივე საზღვრები, ანუ ალგორითმის დასრულებისთვის საჭირო დროის ქვედა და ზედა.
დალაგების მეთოდები Python-ში
Bubble Sort
Bubble Sort არის უმარტივესი გზა მონაცემთა დასალაგებლად რომელიც იყენებს უხეში ძალის ტექნიკას. ის გაიმეორებს მონაცემთა თითოეულ ელემენტს და შეადარებს მას სხვა ელემენტებთანმომხმარებლისთვის დახარისხებული მონაცემების მისაწოდებლად.
მოდით, ავიღოთ მაგალითი ამ ტექნიკის გასაგებად:
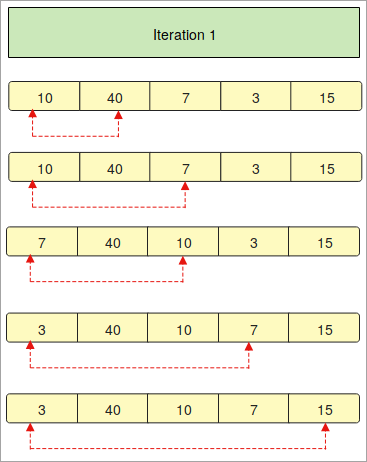
- ჩვენ მოწოდებულია მასივი, რომელსაც აქვს ელემენტები " 10, 40, 7, 3, 15”. ახლა ჩვენ უნდა მოვაწყოთ ეს მასივი აღმავალი თანმიმდევრობით Python-ში Bubble დალაგების ტექნიკის გამოყენებით.
- პირველი ნაბიჯი არის მასივის დალაგება მოცემული თანმიმდევრობით.
- „Iteration 1“-ში ჩვენ სათითაოდ ვადარებთ მასივის პირველ ელემენტს სხვა ელემენტებთან.
- წითელი ისრები აღწერს პირველი ელემენტების შედარებას მასივის სხვა ელემენტებთან.
- თუ შეამჩნევთ, რომ „10“ არის „40“-ზე პატარა, ასე რომ, ის იგივე რჩება. ადგილი, მაგრამ შემდეგი ელემენტი "7" უფრო პატარაა ვიდრე "10". აქედან გამომდინარე, ის იცვლება და პირველ ადგილზე მოდის.
- ზემოხსენებული პროცესი კვლავ და ისევ განხორციელდება ელემენტების დასალაგებლად.
 . 3>
. 3>
-
- „Iteration 2“-ში მეორე ელემენტი შედარებულია მასივის სხვა ელემენტებთან.
- თუ შედარებული ელემენტი მცირეა, მაშინ ის იქნება შეცვალეთ, წინააღმდეგ შემთხვევაში ის დარჩება იმავე ადგილას. მესამე ელემენტი ადარებს მასივის სხვა ელემენტებს. “Iteration 4” მეორე ბოლო ელემენტი შედარებულია მასივის სხვა ელემენტებთან.
- Inამ საფეხურზე მასივი დალაგებულია აღმავალი თანმიმდევრობით.

პროგრამა Bubble დალაგებისთვის
``` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Unsorted List: ", unsorted_list) print("Sorted List using Bubble Sort Technique: ", Bubble_Sort(unsorted_list)) ``` გამომავალი

Bubble-ის დახარისხების დროის სირთულე
- ყველაზე ცუდი შემთხვევა: დროის ყველაზე ცუდი სირთულე ბუშტების დალაგებისთვის არის O( n 2).
- საშუალო შემთხვევა: საშუალო დროის სირთულე ბუშტების დალაგებისთვის არის O( n 2).
- საუკეთესო შემთხვევა: ბუშტების დალაგების საუკეთესო დროის სირთულე არის O(n).
უპირატესობები
- ძირითადად გამოიყენება და მარტივი დასანერგად.
- ჩვენ შეგვიძლია შევცვალოთ მონაცემთა ელემენტები მოკლევადიანი შენახვის გარეშე.
- ეს მოითხოვს ნაკლებს. სივრცე.
მინუსები
- ის არ მუშაობდა დიდი რაოდენობით მონაცემთა ელემენტებთან.
- ის. სჭირდება n 2 ნაბიჯი მონაცემთა ელემენტების თითოეული "n" რაოდენობის დასალაგებლად.
- ეს ნამდვილად არ არის კარგი რეალურ სამყაროში აპლიკაციებისთვის.
ჩასმა. სორტირება
ჩასმის დალაგება არის მარტივი და მარტივი დახარისხების ტექნიკა, რომელიც მუშაობს სათამაშო ბარათების დახარისხების მსგავსად. Insertion sort ახარისხებს ელემენტებს თითოეული ელემენტის სათითაოდ მეორესთან შედარებით. ელემენტები ირჩევა და იცვლება სხვა ელემენტთან, თუ ელემენტი მეორეზე დიდი ან პატარაა.
მოდით ავიღოთ მაგალითი
- ჩვენ მოწოდებულია მასივი, რომელსაც აქვს ელემენტები " 100, 50, 30, 40, 10".
- პირველ რიგში, ვაწყობთ მასივს და ვიწყებთ შედარებასის.
- პირველ საფეხურზე „100“ შედარებულია მეორე ელემენტთან „50“. „50“ იცვლება „100“-ით, რადგან ის უფრო დიდია.
- მეორე საფეხურზე კვლავ მეორე ელემენტი „100“ შედარებულია მესამე ელემენტთან „30“ და ხდება მისი შეცვლა.
- ახლა, თუ შეამჩნევთ, რომ „30“ პირველ ადგილზე მოდის, რადგან ის ისევ „50“-ზე მცირეა.
- შედარება მოხდება მასივის ბოლო ელემენტამდე და ბოლოს მივიღებთ დახარისხებული მონაცემები.

პროგრამა ჩასმის დახარისხებისთვის
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j >= 0 and key_value array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("The unsorted array: ", array) InsertionSort(array) print ("The sorted array using the Insertion Sort: ") for i in range(len(array)): print (array[i]) ``` გამომავალი
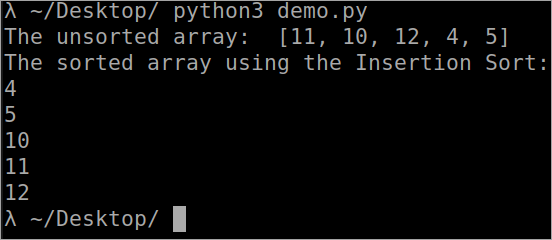
ჩასმის დახარისხების დროის სირთულე
- ყველაზე ცუდი შემთხვევა: ყველაზე ცუდი დროის სირთულე ჩასმის დახარისხებისთვის არის O( n 2).
- საშუალო შემთხვევა: ჩასმის დალაგების საშუალო დროის სირთულე არის O( n 2).
- საუკეთესო შემთხვევა: ჩასმის დალაგების საუკეთესო დროის სირთულე არის O(n).
უპირატესობები
- ეს მარტივია და მარტივი დასანერგად.
- ის კარგად მუშაობს მონაცემთა მცირე რაოდენობის ელემენტებთან მუშაობისას.
- მას არ სჭირდება მეტი სივრცე მისი განხორციელებისთვის.
მინუსები
- არ არის გამოსადეგი მონაცემთა დიდი რაოდენობის დახარისხება.
- დახარისხების სხვა ტექნიკასთან შედარებით, ის კარგად არ მუშაობს.
Merge sort
ეს დახარისხების მეთოდი იყენებს divide and conquer მეთოდს ელემენტების კონკრეტული თანმიმდევრობით დასალაგებლად. შერწყმის დახარისხების დახმარებით დახარისხებისას, აელემენტები იყოფა ნახევრად და შემდეგ, ისინი დალაგებულია. ყველა ნახევრის დალაგების შემდეგ ელემენტები კვლავ უერთდებიან სრულყოფილ წესრიგს.
მოდით ავიღოთ მაგალითი ამ ტექნიკის გასაგებად
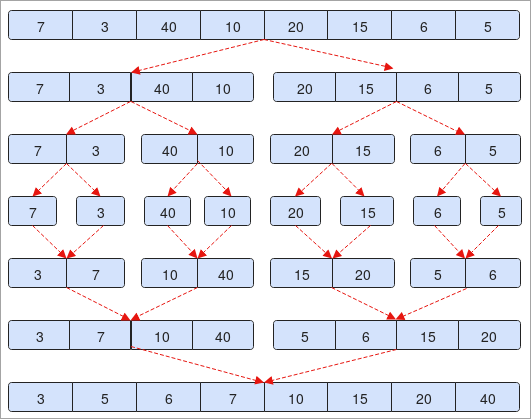
- ჩვენ მოწოდებულია მასივი "7, 3, 40, 10, 20, 15, 6, 5". მასივი შეიცავს 7 ელემენტს. თუ მას გავყოფთ ნახევრად ( 0 + 7 / 2 = 3 ).
- მეორე საფეხურზე ნახავთ, რომ ელემენტები იყოფა ორ ნაწილად. თითოეულს აქვს 4 ელემენტი.
- შემდეგ, ელემენტები კვლავ იყოფა და თითოეულს აქვს 2 ელემენტი.
- ეს პროცესი გაგრძელდება მანამ, სანამ მხოლოდ ერთი ელემენტი იქნება მასივში. იხილეთ ნაბიჯი No. 4 სურათზე.
- ახლა, ჩვენ დავახარისხებთ ელემენტებს და დავიწყებთ მათ შეერთებას ისე, როგორც დავყავით.
- ნაბიჯ No. 5 თუ შეამჩნევთ, რომ 7 3-ზე დიდია, ასე რომ, ჩვენ გავცვლით მათ და ვუერთდებით მას შემდეგ ეტაპზე და პირიქით.
- ბოლოს შეამჩნევთ, რომ ჩვენი მასივი დალაგებულია ზრდის მიხედვით.
პროგრამა შერწყმის დახარისხებისთვის
``` def MergeSort(arr): if len(arr) > 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i len(L) and j len(R): if L[i] R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i len(L): arr[k] = L[i] i += 1 k += 1 while j len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i in range(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Given array is", end="\n") PrintSortedList(arr) MergeSort(arr) print("Sorted array is: ", end="\n") PrintSortedList(arr) ``` გამომავალი
შერწყმის დახარისხების დროის სირთულე
- ყველაზე ცუდი შემთხვევა: შერწყმის დალაგების დროის ყველაზე ცუდი სირთულე არის O( n log( n )).
- საშუალო შემთხვევა: შერწყმის დალაგების საშუალო დროის სირთულე არის O( n log( n )).
- საუკეთესო შემთხვევა: საუკეთესო დროის სირთულე შერწყმის დალაგებისთვის არის O( n log( n )).
უპირატესობები
- ფაილის ზომას მნიშვნელობა არ აქვს დახარისხების ამ ტექნიკისთვის.
- ეს ტექნიკა კარგია იმ მონაცემებისთვის, რომელთა წვდომა ჩვეულებრივ ხდება თანმიმდევრობით. მაგალითად, მიბმული სიები, ფირზე დრაივერი და ა.შ.
მინუსები
- საჭიროებს მეტ სივრცეს სხვასთან შედარებით დახარისხების ტექნიკა.
- ეს შედარებით ნაკლებად ეფექტურია, ვიდრე სხვები.
სწრაფი დახარისხება
სწრაფი დალაგება კვლავ იყენებს გაყოფა და დაამარცხე მეთოდს სიის ელემენტების დასალაგებლად. ან მასივი. ის მიზნად ისახავს საყრდენ ელემენტებს და ახარისხებს ელემენტებს არჩეული საყრდენი ელემენტის მიხედვით.
მაგალითად
- ჩვენ მოწოდებულია მასივი, რომელსაც აქვს ელემენტები “ 1 ,8,3,9,4,5,7 .
- დავუშვათ „7“ საპილოტე ელემენტად.
- ახლა ჩვენ დავყოფთ მასივს ისე, რომ მარცხენა მხარე შეიცავს ელემენტებს, რომლებიც უფრო მცირეა ვიდრე კრებსითი ელემენტი " 7 ", ხოლო მარჯვენა მხარე შეიცავს ელემენტებს უფრო დიდი ვიდრე კრებსითი ელემენტი " 7 ".
- ჩვენ ახლა გვაქვს ორი მასივი " 1,3,4,5 ” და “ 8, 9 “.
- კიდევ ერთხელ, ჩვენ უნდა გავყოთ ორივე მასივი ისევე, როგორც ზემოთ. ერთადერთი განსხვავება ისაა, რომ კრებსითი ელემენტები იცვლება.
- ჩვენ უნდა გავყოთ მასივები მანამ, სანამ არ მივიღებთ მასივის ერთ ელემენტს.
- ბოლოს, შეაგროვეთ ყველა საყრდენი ელემენტი თანმიმდევრობა მარცხნიდან მარჯვნივ და თქვენ მიიღებთ დალაგებასმასივი.
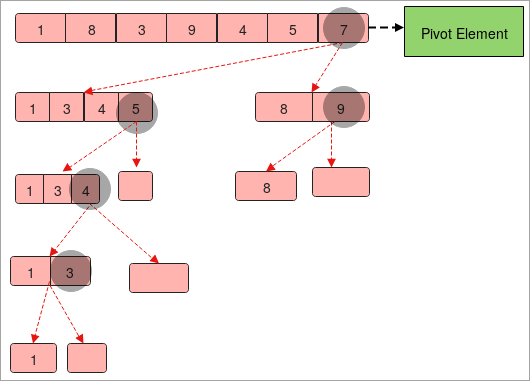
პროგრამა სწრაფი დახარისხებისთვის
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] = pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i ] arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ] return ( i+1 ) def QuickSort( arr, lowest, highest ): if len( arr ) == 1: return arr if lowest highest: pi = Array_Partition( arr, lowest, highest ) QuickSort( arr, lowest, pi-1 ) QuickSort( arr, pi+1, highest ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Unsorted array: ", arr ) QuickSort( arr, 0, n-1 ) print( " Sorted array using Quick Sort: " ) for i in range( n ): print( " %d " % arr[ i ] ) ```
გამომავალი
სწრაფი დახარისხების დროის სირთულე
- ყველაზე ცუდი შემთხვევა: სწრაფი დახარისხების დროის ყველაზე ცუდი სირთულე არის O( n 2).
- საშუალო შემთხვევა: სწრაფი დალაგების საშუალო დროის სირთულე არის O( n log( n ) ).
- საუკეთესო შემთხვევა: საუკეთესო დროის სირთულე სწრაფი დახარისხებისთვის არის O( n log( n )).
უპირატესობები
- იგი ცნობილია, როგორც საუკეთესო დახარისხების ალგორითმი Python-ში.
- ის სასარგებლოა დიდი რაოდენობით მონაცემების დამუშავებისას.
- არ საჭიროებს დამატებით ადგილს.
მინუსები
- მისი ყველაზე უარესი სირთულე მსგავსია ბუშტების დალაგების სირთულეებისა და ჩასმის დალაგება.
- ეს დახარისხების მეთოდი არ არის გამოსადეგი, როცა უკვე გვაქვს დახარისხებული სია.
გროვის დალაგება
Heap sort არის ორობითი საძიებო ხის გაფართოებული ვერსია . გროვის დალაგებისას, მასივის უდიდესი ელემენტი მოთავსებულია ხის ფესვზე ყოველთვის და შემდეგ, ფესვთან შედარებით ფოთლის კვანძებთან.
მაგალითად:
- ჩვენ მოწოდებული გვაქვს მასივი, რომელსაც აქვს ელემენტები " 40, 100, 30, 50, 10".
- " ნაბიჯი 1 " ჩვენ გავაკეთეთ ხე იმის მიხედვით, რომ ელემენტების არსებობა მასივში.

- „ ნაბიჯი 2“ ჩვენ ვაკეთებთ მაქსიმალურ გროვას, ანუ ვაწყობთ ელემენტები კლებადობით. უდიდესი ელემენტი იქნებამდებარეობს ზევით (ფესვი) და ყველაზე პატარა ელემენტი მდებარეობს ბოლოში (ფოთლის კვანძები). მოცემული მასივი ხდება „100, 50, 30, 40, 10“.

- “ ნაბიჯი 3 ” , ჩვენ ვაკეთებთ მინიმალურ გროვას, რათა ვიპოვოთ მასივის მინიმალური ელემენტები. ამით მივიღებთ მაქსიმალურ და მინიმალურ ელემენტებს.

- “ ნაბიჯი 4 ” იგივე ნაბიჯების შესრულებით. ჩვენ ვიღებთ დახარისხებულ მასივს.

პროგრამა გროვის დახარისხებისთვის
``` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left n and arr[ larger_element ] arr[ left ]: larger_element = left if right n and arr[ larger_element ] arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ] HeapSortify( arr, n, larger_element ) def HeapSort( arr ): n = len( arr ) for i in range( n//2 - 1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " The unsorted array is: ", arr ) HeapSort( arr ) n = len( arr ) print( " The sorted array sorted by the Heap Sort: " ) for i in range( n ): print( arr[ i ] ) ```
გამომავალი
გროვის დალაგების დროის სირთულე
- ყველაზე ცუდი შემთხვევა: დაგროვების დახარისხების დროის ყველაზე ცუდი სირთულე არის O( n log( n )).
- საშუალო შემთხვევა: გროვის დალაგების საშუალო დროის სირთულე არის O( n log( n )).
- საუკეთესო შემთხვევა: საუკეთესო დროის სირთულე გროვის დახარისხებისთვის isO( n log( n )).
უპირატესობები
- იგი ძირითადად გამოიყენება პროდუქტიულობის გამო.
- მას შეუძლია განხორციელდეს როგორც ადგილზე ალგორითმი.
- არ საჭიროებს დიდ მეხსიერებას.
მინუსები
- საჭიროებს სივრცეს ელემენტების დახარისხება.
- ის ქმნის ხეს ელემენტების დასალაგებლად.
დახარისხების ტექნიკას შორის შედარება
| დახარისხების მეთოდი | საუკეთესო შემთხვევის დროის სირთულე | საშუალო შემთხვევათა დროის სირთულე | უარეს შემთხვევაში დროის სირთულე | სივრცის სირთულე | სტაბილურობა | ში - |
|---|