Ismerje meg, hogyan használja a Python Sort függvényt listák, tömbök, szótárak stb. rendezésére különböző rendezési módszerek és algoritmusok segítségével Pythonban:
A rendezés olyan technika, amelyet az adatok sorrendbe rendezésére használnak, akár növekvő, akár csökkenő sorrendben.
A nagy projektek adatai legtöbbször nincsenek a megfelelő sorrendben, és ez problémákat okoz a szükséges adatok hatékony elérése és lekérése során.
A Python különböző rendezési technikákat kínál, amelyek segítségével megoldható ez a probléma. például, Bubble sort, Insertion sort, Merge sort, Quicksort stb.
Ebben a bemutatóban megértjük, hogyan működik a Pythonban a rendezés különböző algoritmusok segítségével.
Python Sort

A Python Sort szintaxisa
A rendezéshez a Python beépített függvényt biztosít, a " sort() " függvényt, amely egy lista adatelemeinek növekvő vagy csökkenő sorrendbe rendezésére szolgál.
Értsük meg ezt a fogalmat egy példán keresztül.
Példa 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( " List in ascending order: ", a ) ```
Kimenet:

Ebben a példában a megadott rendezetlen listát a " sort( ) " függvény segítségével növekvő sorrendbe rendezzük.
2. példa:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( " Lista csökkenő sorrendben: ", a ) ```
Kimenet

A fenti példában az adott rendezetlen listát a " sort( reverse = True ) " függvény segítségével fordított sorrendbe rendezzük.
A rendező algoritmusok időbonyolultsága
Az időbonyolultság az az idő, amely alatt a számítógép egy adott algoritmus futtatásához szükséges. Az időbonyolultságnak háromféle esete van.
- Legrosszabb esetben: A számítógép által a program futtatásához szükséges maximális idő.
- Átlagos eset: A számítógép által a program futtatásához a minimum és a maximum között eltelt idő.
- Legjobb esetben: A számítógép által a program futtatásához szükséges minimális idő. Ez az időbonyolultság legjobb esete.
Komplexitás jelölések
Big Oh Notation, O: A Big oh jelölés a hivatalos módja az algoritmusok futási idejének felső korlátjának megadására. A legrosszabb esetre vonatkozó időbonyolultság mérésére szolgál, vagy úgy mondjuk, hogy az algoritmus által a legnagyobb időigényt jelenti.
Nagy omega jelölés,  : A nagy omega jelölés a hivatalos módja annak, hogy az algoritmusok futási idejének legalacsonyabb korlátját közvetítsük. A legjobb eset időbonyolultságának mérésére használják, vagy azt mondjuk, hogy az algoritmus által eltöltött kiváló idő.
: A nagy omega jelölés a hivatalos módja annak, hogy az algoritmusok futási idejének legalacsonyabb korlátját közvetítsük. A legjobb eset időbonyolultságának mérésére használják, vagy azt mondjuk, hogy az algoritmus által eltöltött kiváló idő.
Théta jelölés, 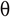 : A théta jelölés a hivatalos módja annak, hogy az algoritmus által az algoritmus befejezéséhez szükséges idő alsó és felső határértékét is megadjuk.
: A théta jelölés a hivatalos módja annak, hogy az algoritmus által az algoritmus befejezéséhez szükséges idő alsó és felső határértékét is megadjuk.
Rendezési módszerek Pythonban
Buborék rendezés
A buborékos rendezés a legegyszerűbb módja az adatok rendezésének, amely a nyers erő technikát használja. Minden egyes adatelemet végigjár, és összehasonlítja más elemekkel, hogy a felhasználónak a rendezett adatokat adja meg.
Vegyünk egy példát ennek a technikának a megértéséhez:
- Kapunk egy tömböt, amelynek elemei " 10, 40, 7, 3, 15 ". Most ezt a tömböt növekvő sorrendbe kell rendeznünk a Python Bubble sort technikájával.
- A legelső lépés az, hogy a tömböt a megadott sorrendbe rendezzük.
- Az " Iteráció 1 " során egy tömb első elemét egyenként összehasonlítjuk a többi elemmel.
- A piros nyilak az első elemek összehasonlítását írják le a tömb többi elemével.
- Ha észrevesszük, hogy a " 10 " kisebb, mint a " 40 ", tehát ugyanott marad, de a következő elem " 7 " kisebb, mint a " 10 ". Ezért kicserélődik és az első helyre kerül.
- A fenti folyamatot újra és újra el kell végezni az elemek rendezéséhez.
- A " 2. ismétlés " során a második elemet összehasonlítjuk a tömb többi elemével.
- Ha az összehasonlított elem kicsi, akkor kicserélődik, különben ugyanott marad.

- A " 3. ismétlés " során a harmadik elemet összehasonlítjuk a tömb többi elemével.

- Az utolsó " Iteráció 4 " az utolsó előtti elemet hasonlítjuk össze a tömb többi elemével.
- Ebben a lépésben a tömböt növekvő sorrendbe rendezzük.

Program a Bubble rendezéshez
``` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Rendezetlen lista: ", unsorted_list) print("Rendezett lista Bubble Sort segítségével.Technika: ", Bubble_Sort(unsorted_list)) ``` Kimenet

A Bubble sort időbeli összetettsége
- Legrosszabb esetben: A buborékrendezés legrosszabb időbonyolultsága O( n 2).
- Átlagos eset: A buborékválogatás átlagos időbonyolultsága O( n 2).
- Legjobb esetben: A legjobb időbonyolultság a buborékválogatáshoz O(n).
Előnyök
- Leggyakrabban használják, és könnyen megvalósítható.
- Az adatelemeket a rövid távú tárolás igénybevétele nélkül cserélhetjük.
- Kevesebb helyet igényel.
Hátrányok
- Nem teljesített jól, amikor nagyszámú nagy adatelemet kezelt.
- Szüksége van n 2 lépés minden egyes "n" számú adatelemhez, amelyet rendezni kell.
- Ez nem igazán jó a valós alkalmazásokhoz.
Beillesztés Rendezés
A beillesztési rendezés egy könnyű és egyszerű rendezési technika, amely a játékkártyák rendezéséhez hasonlóan működik. A beillesztési rendezés úgy rendezi az elemeket, hogy az egyes elemeket egyenként összehasonlítja a másikkal. Az elemeket kiválasztja és kicseréli a másik elemmel, ha az elem nagyobb vagy kisebb, mint a másik.
Vegyünk egy példát
- Kapunk egy tömböt, amelynek elemei " 100, 50, 30, 40, 10 ".
- Először rendezzük el a tömböt, és kezdjük el az összehasonlítást.
- Az első lépésben a " 100 " értéket összehasonlítjuk a második " 50 " elemmel. " 50 " értéket felcseréljük a " 100 " értékkel, mivel az nagyobb.
- A második lépésben a második " 100 " elemet ismét összehasonlítjuk a harmadik " 30 " elemmel, és felcseréljük.
- Most, ha észreveszed, a " 30 " az első helyre kerül, mert ismét kisebb, mint az " 50 ".
- Az összehasonlítás a tömb utolsó eleméig történik, és a végén megkapjuk a rendezett adatokat.

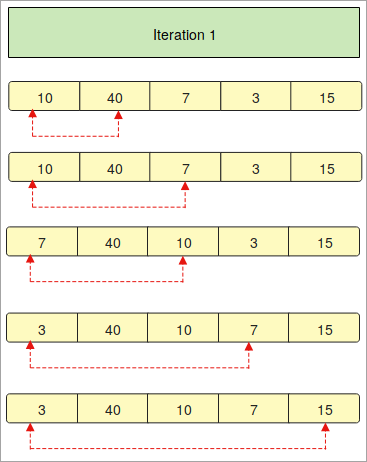
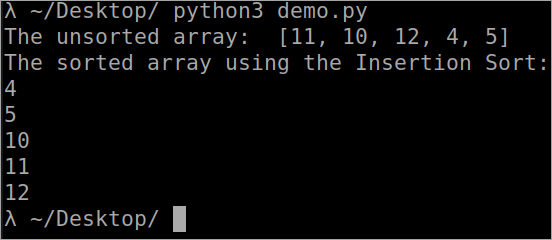
Program a beillesztési rendezéshez
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j>= 0 and key_value <array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("A rendezetlen array: ", array) InsertionSort(array) print ("A rendezett array az Insertion Sort segítségével: ") for i in range(len(array)): print (array[i]) ```` Kimenet
A beillesztési fajta időbeli összetettsége
- Legrosszabb esetben: Az Insertion sort legrosszabb időigénye O( n 2).
- Átlagos eset: Az Insertion sort átlagos időbonyolultsága O( n 2).
- Legjobb esetben: A legjobb időbonyolítás az Insertion sort esetében O(n).
Előnyök
- Egyszerű és könnyen megvalósítható.
- Jól teljesít kisszámú adatelemek kezelése során.
- Nincs szüksége több helyre a megvalósításához.
Hátrányok
- Nem hasznos a nagyszámú adatelem rendezése.
- Más válogatási technikákkal összehasonlítva nem teljesít jól.
Összevonás rendezés
Ez a rendezési módszer az oszd meg és uralkodj módszert használja az elemek meghatározott sorrendbe rendezéséhez. Az egyesített rendezéssel történő rendezés során az elemeket felekre osztják, majd rendezik őket. Az összes fél rendezése után az elemeket ismét egyesítik, hogy tökéletes sorrendet alkossanak.
Vegyünk egy példát, hogy megértsük ezt a technikát
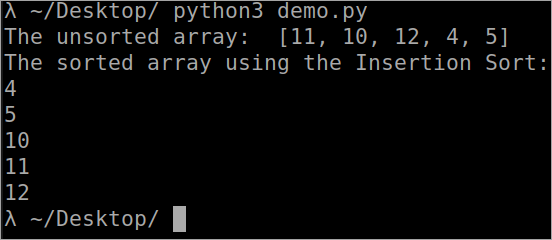
- Kapunk egy tömböt " 7, 3, 40, 10, 20, 15, 6, 5 ". A tömb 7 elemet tartalmaz. Ha felére osztjuk ( 0 + 7 / 2 = 3 ).
- A második lépésben látni fogod, hogy az elemek két részre vannak osztva. Mindegyikben 4 elem van.
- Továbbá, az elemek ismét fel vannak osztva, és egyenként 2 elemet tartalmaznak.
- Ez a folyamat addig folytatódik, amíg csak egy elem van a tömbben. Lásd a 4. lépést a képen.
- Most rendezni fogjuk az elemeket, és elkezdjük összekapcsolni őket, ahogyan osztottuk.
- Az 5. lépésben, ha észreveszed, hogy a 7 nagyobb, mint a 3, akkor kicseréljük őket, és a következő lépésben csatlakozunk hozzá, és fordítva.
- A végén észrevehetjük, hogy a tömbünk növekvő sorrendbe rendeződik.
Program a Merge rendezéshez
``` def MergeSort(arr): if len(arr)> 1: közép = len(arr)//2 L = arr[:közép] R = arr[közép:] MergeSort(L) MergeSort(L) MergeSort(R) i = j = k = 0 while i <len(L) and j <len(R): if L[i] <R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i <len(L): arr[k] = L[i] i += 1 k += 1 while j <len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i inrange(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Adott tömb", end="\n") PrintSortedList(arr) MergeSort(arr) print("Rendezett tömb: ", end="\n") PrintSortedList(arr) ``` Kimenet
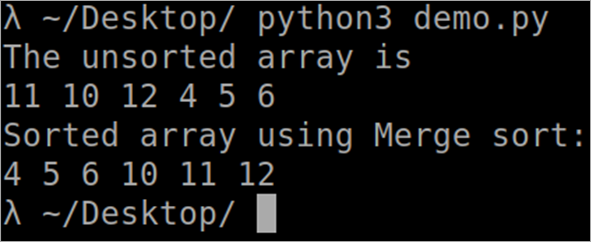
Az összevonási rendezés időbeli bonyolultsága
- Legrosszabb esetben: A legrosszabb időbonyolultság az egyesített rendezésnél O( n log( n )).
- Átlagos eset: Az átlagos időbonyolultság az egyesített rendezéshez O( n log( n )).
- Legjobb esetben: A legjobb időbonyolultság az egyesített rendezéshez O( n log( n )).
Előnyök
- A fájl mérete nem számít ennél a rendezési technikánál.
- Ez a technika az olyan adatok esetében jó, amelyekhez általában sorrendben férünk hozzá. Például, összekapcsolt listák, szalagmeghajtó stb.
Hátrányok
- Több helyet igényel, mint más válogatási technikák.
- Viszonylag kevésbé hatékony, mint mások.
Gyors válogatás
A gyors rendezés ismét az oszd meg és uralkodj módszert használja egy Lista vagy tömb elemeinek rendezésére. Megcélozza a sarkalatos elemeket, és a kiválasztott sarkalatos elem szerint rendezi az elemeket.
Például
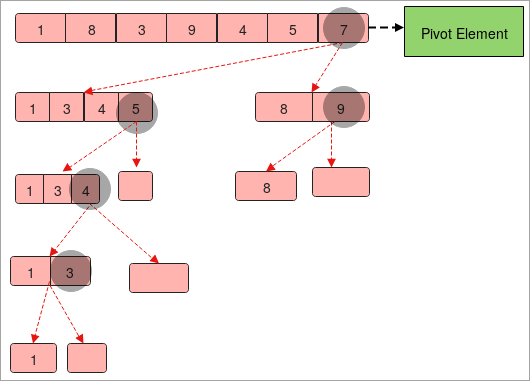
- Kapunk egy tömböt, amelynek elemei: " 1,8,3,9,4,5,7 ".
- Tegyük fel, hogy a " 7 " egy kísérleti elem.
- Most úgy osztjuk fel a tömböt, hogy a bal oldali rész tartalmazza a " 7 " pivot elemnél kisebb elemeket, a jobb oldali rész pedig a " 7 " pivot elemnél nagyobb elemeket.
- Most már két tömbünk van: " 1,3,4,5 " és " 8, 9 ".
- Ismét mindkét tömböt ugyanúgy kell felosztanunk, mint fentebb. Az egyetlen különbség az, hogy a pivot elemek megváltoznak.
- A tömböket addig kell osztanunk, amíg egyetlen elemet nem kapunk a tömbben.
- A végén gyűjtsd össze az összes pivot elemet balról jobbra haladva, és megkapod a rendezett tömböt.
Program gyors rendezéshez
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] <= pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i ] arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ] return ( i+1 ) def QuickSort( arr, lowest, highest ): if len( arr ) == 1: return arr if lowest <highest: pi = Array_Partition(arr, legalacsonyabb, legmagasabb ) QuickSort( arr, legalacsonyabb, pi-1 ) QuickSort( arr, pi+1, legmagasabb ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Rendezetlen tömb: ", arr ) QuickSort( arr, 0, n-1 ) print( " Rendezett tömb Quick Sort segítségével: " ) for i in range( n ): print( " %d " % arr[ i ] ) ```
Kimenet
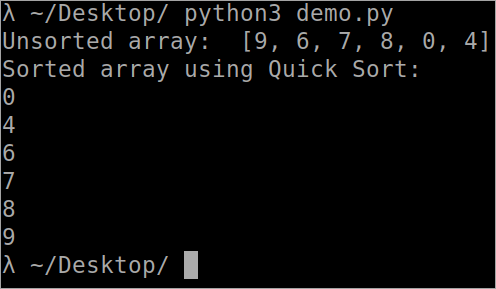
A gyors válogatás időbeli összetettsége
- Legrosszabb esetben: A Quick sort legrosszabb időigénye O( n 2).
- Átlagos eset: A Quick sort átlagos időigénye O( n log( n )).
- Legjobb esetben: A Quick sort legjobb időbonyolultsága O( n log( n )).
Előnyök
- A Python legjobb rendező algoritmusaként ismert.
- Hasznos nagy mennyiségű adat kezelése során.
- Nem igényel további helyet.
Hátrányok
- A legrosszabb esetben hasonlóan bonyolult, mint a buborékválogatás és a beszúrásválogatás.
- Ez a rendezési módszer nem hasznos, ha már megvan a rendezett lista.
Halom rendezés
A halomrendezés a bináris keresési fa továbbfejlesztett változata. A halomrendezésben egy tömb legnagyobb elemét mindig a fa gyökerére helyezzük, majd a gyökeret a levélcsomópontokkal hasonlítjuk össze.
Például:
- Kapunk egy tömböt, amelynek elemei " 40, 100, 30, 50, 10 ".
- A oldalon. " 1. lépés " a tömb elemeinek jelenléte szerint készítettünk egy fát.

- A " 2. lépés " maximális halmazt készítünk, azaz az elemeket csökkenő sorrendbe rendezzük. A legnagyobb elem a tetején (gyökér), a legkisebb elem pedig az alján (levélcsomópontok) lesz. A megadott tömb " 100, 50, 30, 40, 10 " lesz.

- A oldalon. " 3. lépés " , a minimális halmazt készítjük el, hogy megtaláljuk egy tömb minimális elemeit. Ezzel megkapjuk a maximális és a minimális elemeket.

- A oldalon. " 4. lépés " ugyanezeket a lépéseket végrehajtva megkapjuk a rendezett tömböt.

Program a Heap rendezéshez
``` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left <n és arr[ larger_element ] <arr[ left ]: larger_element = left if right <n és arr[ larger_element ] <arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ] HeapSortify( arr, n, larger_element ) def HeapSort( arr): n = len( arr ) for i in range( n//2 - 1, -1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " The unsorted array is: ", arr ) HeapSort( arr ) n = len( arr ) print( " The sorted array sorted by the Heap Sort: " ) for i in range( n ): print( arr[ i ] ) ````
Kimenet
A halom rendezés időbeli bonyolultsága
- Legrosszabb esetben: A Heap sort legrosszabb időbonyolultsága O( n log( n )).
- Átlagos eset: A Heap sort átlagos időigénye O( n log( n )).
- Legjobb esetben: A legjobb időbonyolultság a Heap rendezéshezO( n log( n )).
Előnyök
- Leginkább termelékenysége miatt használják.
- Ez egy in-place algoritmusként is megvalósítható.
- Nem igényel nagy tárolót.
Hátrányok
- Helyre van szükség az elemek rendezéséhez.
- Ez teszi a fát az elemek rendezéséhez.
A válogatási technikák összehasonlítása
| Válogatási módszer | Legjobb esetben időbeli összetettség | Az eset átlagos időbeli összetettsége | Legrosszabb esetben időbeli összetettség | Térbeli komplexitás | Stabilitás | Helyben - helyben |
|---|---|---|---|---|---|---|
| Buborék válogatás | O(n) | O(n2) | O(n2) | O(1) | Igen | Igen |
| Beillesztési rendezés | O(n) | O(n2) | O(n2) | O(1) | Igen | Igen |
| Gyors válogatás | O(n log(n)) | O(n log(n)) | O(n2) | O(N) | Nem | Igen |
| Összevonás rendezés | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(N) | Igen | Nem |
| Halom rendezés | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) | Nem | Igen |
A fenti összehasonlító táblázatban az " O " a fentebb ismertetett Big Oh jelölés, míg az " n " és " N " a bemenet méretét jelenti.
Gyakran ismételt kérdések
K #1) Mi az a sort () Pythonban?
Válasz: A Pythonban a sort() egy olyan függvény, amely a listák vagy tömbök meghatározott sorrendbe rendezésére szolgál. Ez a függvény megkönnyíti a rendezés folyamatát a nagy projektek munkája során. Nagyon hasznos a fejlesztők számára.
K #2) Hogyan lehet Pythonban rendezni?
Válasz: A Python különböző rendezési technikákat biztosít, amelyeket az elem rendezésére használnak. Például, Gyors rendezés, Összevonás rendezés, Buborék rendezés, Beillesztés rendezés, stb. Minden rendezési technika hatékony és könnyen érthető.
K #3) Hogyan működik a Python sort ()?
Válasz: A sort() függvény a megadott tömböt a felhasználó bemeneteként veszi, és a rendezési algoritmus segítségével egy adott sorrendbe rendezi. Az algoritmus kiválasztása a felhasználó választásától függ. A felhasználók használhatják a Quick sort, Merge sort, Bubble sort, Insertion sort, stb. a felhasználó igényeitől függően.
Következtetés
A fenti bemutatóban az általános rendezési technikákkal együtt a Pythonban a rendezési technikát is tárgyaltuk.
- Buborék rendezés
- Beillesztés Rendezés
- Gyors szortírozás
Megismertük az időbeli összetettségüket, előnyeiket és hátrányaikat. Összehasonlítottuk a fenti technikákat is.