पायथन में विभिन्न सॉर्टिंग विधियों और एल्गोरिदम का उपयोग करके सूचियों, सरणियों, शब्दकोशों आदि को सॉर्ट करने के लिए पायथन सॉर्ट फ़ंक्शन का उपयोग करना सीखें:
सॉर्टिंग एक ऐसी तकनीक है जिसका उपयोग सॉर्टिंग के लिए किया जाता है आरोही या अवरोही क्रम में एक अनुक्रम क्रम में डेटा।
अधिकांश समय बड़ी परियोजनाओं के डेटा को सही क्रम में व्यवस्थित नहीं किया जाता है और यह आवश्यक डेटा को कुशलतापूर्वक एक्सेस करने और प्राप्त करने में समस्या पैदा करता है।
इस समस्या को हल करने के लिए छँटाई तकनीकों का उपयोग किया जाता है। पायथन विभिन्न सॉर्टिंग तकनीक प्रदान करता है उदाहरण के लिए, बबल सॉर्ट, इंसर्शन सॉर्ट, मर्ज सॉर्ट, क्विकसॉर्ट आदि।
इस ट्यूटोरियल में, हम समझेंगे कि विभिन्न एल्गोरिदम का उपयोग करके पायथन में सॉर्टिंग कैसे काम करती है।
पायथन सॉर्ट

पायथन सॉर्ट का सिंटैक्स
छँटाई करने के लिए, पायथन बिल्ट-इन फ़ंक्शन प्रदान करता है, अर्थात "सॉर्ट ()" फ़ंक्शन। इसका उपयोग किसी सूची के डेटा तत्वों को आरोही क्रम या अवरोही क्रम में क्रमबद्ध करने के लिए किया जाता है।
आइए इस अवधारणा को एक उदाहरण से समझते हैं।
उदाहरण 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( “ List in ascending order: ”, a ) ```
आउटपुट:

इस उदाहरण में, दी गई अनियंत्रित सूची को "सॉर्ट ()" फ़ंक्शन का उपयोग करके आरोही क्रम में क्रमबद्ध किया गया है .
उदाहरण 2:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( “ List in descending order: ”, a ) ```
आउटपुट

उपरोक्त उदाहरण में, दी गई अनियंत्रित सूची को "सॉर्ट (रिवर्स = ट्रू)" फ़ंक्शन का उपयोग करके रिवर्स ऑर्डर में सॉर्ट किया गया है।
समयजगह बबल सॉर्ट O(n) O(n2) O(n2) O(1) हां हां इंसर्शन सॉर्ट 42 ओ(एन) ओ(एन2) ओ(एन2) ओ(1) हां हां त्वरित सॉर्ट O(n log(n)) O(n log(n)) ओ(एन2) ओ(एन) नहीं हां मर्ज करें क्रमबद्ध करें ओ(एन लॉग(एन)) ओ(एन लॉग(एन)) ओ(एन लॉग(एन)) O(N) हां नहीं हीप सॉर्ट O(n लॉग (एन)) ओ(एन लॉग(एन)) ओ(एन लॉग(एन)) ओ(1) नहीं हां
उपरोक्त तुलना तालिका में "ओ" बिग ओह नोटेशन है जिसे ऊपर समझाया गया है जबकि "एन" और "एन" का अर्थ इनपुट का आकार है .
अक्सर पूछे जाने वाले प्रश्न
प्रश्न #1) पायथन में सॉर्ट () क्या है?
उत्तर: पायथन में सॉर्ट () एक ऐसा फ़ंक्शन है जिसका उपयोग किसी विशिष्ट क्रम में सूचियों या सरणियों को क्रमबद्ध करने के लिए किया जाता है। यह फ़ंक्शन बड़ी परियोजनाओं पर काम करते समय छँटाई की प्रक्रिया को आसान बनाता है। यह डेवलपर्स के लिए बहुत मददगार है।
क्यू #2) आप पायथन में कैसे सॉर्ट करते हैं?
उत्तर: Python विभिन्न सॉर्टिंग तकनीकें प्रदान करता है जिनका उपयोग तत्वों को सॉर्ट करने के लिए किया जाता है। उदाहरण के लिए, क्विक सॉर्ट, मर्ज सॉर्ट, बबल सॉर्ट, इंसर्शन सॉर्ट आदि। सभी सॉर्टिंग तकनीक कुशल और समझने में आसान हैं।
क्यू #3) पायथन कैसे करता है सॉर्ट () काम?
उत्तर: छँटाई ()फ़ंक्शन दिए गए सरणी को उपयोगकर्ता से इनपुट के रूप में लेता है और सॉर्टिंग एल्गोरिदम का उपयोग करके इसे एक विशिष्ट क्रम में सॉर्ट करता है। एल्गोरिदम का चयन उपयोगकर्ता की पसंद पर निर्भर करता है। उपयोगकर्ता अपनी आवश्यकताओं के आधार पर क्विक सॉर्ट, मर्ज सॉर्ट, बबल सॉर्ट, इंसर्शन सॉर्ट आदि का उपयोग कर सकते हैं।
निष्कर्ष
उपरोक्त ट्यूटोरियल में, हमने पायथन में सॉर्ट तकनीक के साथ-साथ चर्चा की सामान्य सॉर्टिंग तकनीकें।
- बबल सॉर्ट
- इंसर्शन सॉर्ट
- क्विक सॉर्ट
हमने उनके समय की जटिलताओं और फायदों के बारे में सीखा और; कमियां। हमने उपरोक्त सभी तकनीकों की तुलना भी की।
छँटाई एल्गोरिदम की जटिलतासमय जटिलता कंप्यूटर द्वारा किसी विशेष एल्गोरिदम को चलाने में लगने वाले समय की मात्रा है। इसमें समय जटिलता के तीन प्रकार के मामले हैं।
- सबसे खराब स्थिति: कार्यक्रम को चलाने के लिए कंप्यूटर द्वारा लिया गया अधिकतम समय।
- औसत मामला: प्रोग्राम को चलाने के लिए कंप्यूटर द्वारा न्यूनतम और अधिकतम के बीच लिया गया समय।
- सर्वश्रेष्ठ मामला: प्रोग्राम को चलाने के लिए कंप्यूटर द्वारा लिया गया न्यूनतम समय। यह समय जटिलता का सबसे अच्छा मामला है।
जटिलता संकेतन
बिग ओह नोटेशन, ओ: बिग ओह नोटेशन ऊपरी सीमा को व्यक्त करने का आधिकारिक तरीका है एल्गोरिदम के चलने का समय। इसका उपयोग सबसे खराब समय की जटिलता को मापने के लिए किया जाता है या हम कहते हैं कि एल्गोरिथम को पूरा करने में लगने वाला सबसे बड़ा समय है।
बिग ओमेगा नोटेशन,  : बिग ओमेगा नोटेशन है एल्गोरिदम के चलने के समय की निम्नतम सीमा को व्यक्त करने का आधिकारिक तरीका। इसका उपयोग बेस्ट-केस टाइम जटिलता को मापने के लिए किया जाता है या हम कहते हैं कि एल्गोरिथम द्वारा लिया गया उत्कृष्ट समय है। एल्गोरिथम द्वारा पूरा होने में लगने वाले समय के निचले और ऊपरी दोनों बाउंड्स। जो ब्रूट फोर्स तकनीक का उपयोग करता है। यह प्रत्येक डेटा तत्व के लिए पुनरावृति करेगा और अन्य तत्वों के साथ इसकी तुलना करेगाउपयोगकर्ता को क्रमबद्ध डेटा प्रदान करने के लिए।
: बिग ओमेगा नोटेशन है एल्गोरिदम के चलने के समय की निम्नतम सीमा को व्यक्त करने का आधिकारिक तरीका। इसका उपयोग बेस्ट-केस टाइम जटिलता को मापने के लिए किया जाता है या हम कहते हैं कि एल्गोरिथम द्वारा लिया गया उत्कृष्ट समय है। एल्गोरिथम द्वारा पूरा होने में लगने वाले समय के निचले और ऊपरी दोनों बाउंड्स। जो ब्रूट फोर्स तकनीक का उपयोग करता है। यह प्रत्येक डेटा तत्व के लिए पुनरावृति करेगा और अन्य तत्वों के साथ इसकी तुलना करेगाउपयोगकर्ता को क्रमबद्ध डेटा प्रदान करने के लिए।
आइए इस तकनीक को समझने के लिए एक उदाहरण लेते हैं:
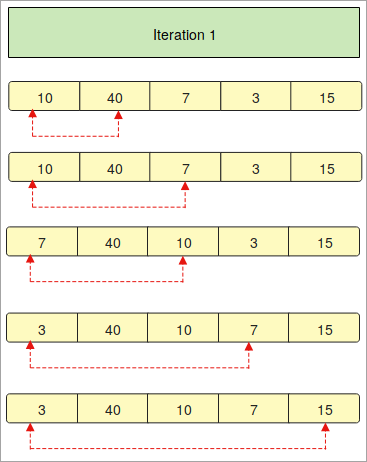
- हमें तत्वों के साथ एक सरणी प्रदान की जाती है 10, 40, 7, 3, 15 ”। अब, हमें पायथन में बबल सॉर्ट तकनीक का उपयोग करके इस सरणी को आरोही क्रम में व्यवस्थित करने की आवश्यकता है।
- दिए गए क्रम में सरणी को व्यवस्थित करने के लिए सबसे पहला कदम है।
- “पुनरावृत्ति 1” में, हम एक सरणी के पहले तत्व की अन्य तत्वों के साथ एक-एक करके तुलना कर रहे हैं।
- लाल तीर किसी सरणी के अन्य तत्वों के साथ पहले तत्वों की तुलना का वर्णन कर रहे हैं।
- यदि आप देखते हैं कि "10" "40" से छोटा है, तो यह समान रहता है जगह लेकिन अगला तत्व "7" "10" से छोटा है। इसलिए यह बदल जाता है और पहले स्थान पर आ जाता है।
- उपरोक्त प्रक्रिया बार-बार तत्वों को क्रमबद्ध करने के लिए की जाएगी।
-
- “पुनरावृत्ति 2” में दूसरे तत्व की तुलना किसी सरणी के अन्य तत्वों से की जा रही है।
- यदि तुलना किया गया तत्व छोटा है, तो यह होगा बदल लें, अन्यथा यह उसी स्थान पर रहेगा। तीसरे तत्व की तुलना किसी सरणी के अन्य तत्वों से की जा रही है।

-
- अंतिम में "पुनरावृत्ति 4" दूसरे अंतिम तत्व की तुलना किसी सरणी के अन्य तत्वों से की जा रही है।
- मेंइस चरण में सरणी को आरोही क्रम में क्रमबद्ध किया गया है। 0> आउटपुट

बबल सॉर्ट की समय जटिलता
- सबसे खराब स्थिति: बबल सॉर्ट के लिए सबसे खराब समय जटिलता O( n 2) है।
- औसत मामला: बबल सॉर्ट के लिए औसत समय जटिलता O(4) है>n 2).
- सबसे अच्छा मामला: बबल सॉर्ट के लिए सबसे अच्छा समय जटिलता O(n) है।
फायदे
- यह ज्यादातर उपयोग किया जाता है और इसे लागू करना आसान है।
- हम डेटा तत्वों को अल्पकालिक भंडारण की खपत के बिना स्वैप कर सकते हैं।
- इसके लिए कम आवश्यकता होती है स्पेस।
नुकसान
- बड़ी संख्या में डेटा तत्वों से निपटने के दौरान इसने अच्छा प्रदर्शन नहीं किया।
- यह सॉर्ट करने के लिए प्रत्येक "n" संख्या के डेटा तत्वों के लिए n 2 चरणों की आवश्यकता होती है।
- यह वास्तविक दुनिया के अनुप्रयोगों के लिए वास्तव में अच्छा नहीं है।
सम्मिलन सॉर्ट
इंसर्शन सॉर्ट एक आसान और सरल सॉर्टिंग तकनीक है जो प्लेइंग कार्ड्स को सॉर्ट करने के समान काम करती है। इंसर्शन सॉर्ट प्रत्येक तत्व की एक-एक करके दूसरे के साथ तुलना करके तत्वों को क्रमबद्ध करता है। यदि तत्व दूसरे से बड़ा या छोटा है तो तत्वों को चुना जाता है और दूसरे तत्व के साथ स्वैप किया जाता है।
आइए एक उदाहरण लें
- हमें प्रदान किया गया एक सरणी जिसमें "100, 50, 30, 40, 10" तत्व हैं।
- सबसे पहले, हम सरणी को व्यवस्थित करते हैं और तुलना करना शुरू करते हैंयह.
- पहले चरण में “100” की तुलना दूसरे तत्व “50” से की जाती है। “50” को “100” से स्वैप किया जाता है क्योंकि यह अधिक है।
- दूसरे चरण में, फिर से दूसरे तत्व “100” की तुलना तीसरे तत्व “30” से की जाती है और इसे स्वैप किया जाता है।
- अब, यदि आप देखते हैं कि "30" पहले स्थान पर आता है क्योंकि यह फिर से "50" से छोटा है।
- तुलना किसी सरणी के अंतिम तत्व तक होगी और अंत में, हमें सॉर्ट किया गया डेटा।

इंसर्शन सॉर्ट के लिए प्रोग्राम
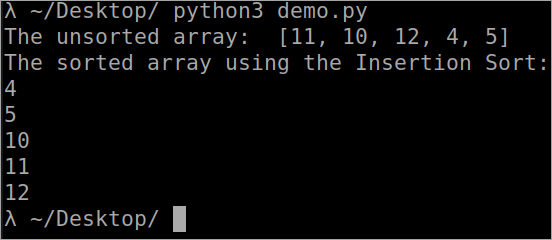
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j >= 0 and key_value array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("The unsorted array: ", array) InsertionSort(array) print ("The sorted array using the Insertion Sort: ") for i in range(len(array)): print (array[i]) ```आउटपुट
0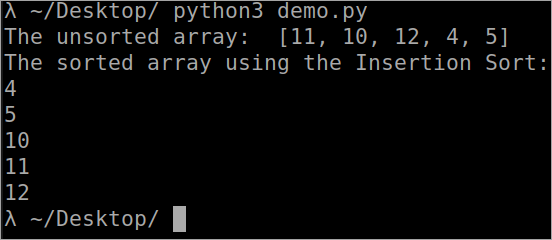
प्रविष्टि छँटाई की समय जटिलता
- सबसे खराब स्थिति: सम्मिलन छँटाई के लिए सबसे खराब समय जटिलता O( n 2).
- औसत मामला: सम्मिलन सॉर्ट के लिए औसत समय जटिलता O( n 2) है।
- सर्वश्रेष्ठ स्थिति: निवेशन क्रम के लिए सर्वोत्तम समय जटिलता O(n) है।
लाभ
- यह सरल है और लागू करने में आसान।
- डेटा तत्वों की एक छोटी संख्या के साथ व्यवहार करते समय यह अच्छा प्रदर्शन करता है।
- इसके कार्यान्वयन के लिए इसे और अधिक स्थान की आवश्यकता नहीं है।
नुकसान
- बड़ी संख्या में डेटा तत्वों को क्रमबद्ध करना सहायक नहीं है।
- अन्य छँटाई तकनीकों की तुलना में यह अच्छा प्रदर्शन नहीं करता है।
मर्ज सॉर्ट
यह सॉर्टिंग विधि तत्वों को एक विशिष्ट क्रम में सॉर्ट करने के लिए विभाजित और जीतना विधि का उपयोग करती है। मर्ज सॉर्ट की मदद से सॉर्ट करते समय,तत्वों को हिस्सों में विभाजित किया जाता है और फिर उन्हें क्रमबद्ध किया जाता है। सभी हिस्सों को छांटने के बाद, फिर से तत्व एक पूर्ण क्रम बनाने के लिए जुड़ जाते हैं।
इस तकनीक को समझने के लिए एक उदाहरण लेते हैं
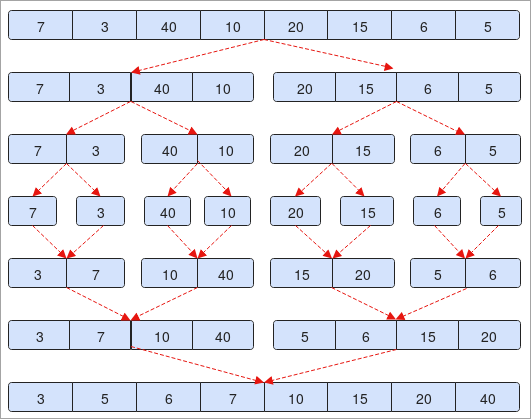
- हमें इसके साथ प्रदान किया गया है एक सरणी "7, 3, 40, 10, 20, 15, 6, 5"। सरणी में 7 तत्व होते हैं। यदि हम इसे आधे में विभाजित करें ( 0 + 7 / 2 = 3 )।
- दूसरे चरण में, आप देखेंगे कि तत्व दो भागों में विभाजित हैं। प्रत्येक में 4 तत्व होते हैं।
- इसके अलावा, तत्वों को फिर से विभाजित किया जाता है और प्रत्येक में 2 तत्व होते हैं।
- यह प्रक्रिया तब तक जारी रहेगी जब तक कि एक सरणी में केवल एक तत्व मौजूद न हो। चरण संख्या का संदर्भ लें। चित्र में 4।
- अब, हम तत्वों को क्रमबद्ध करेंगे और उन्हें विभाजित करना शुरू करेंगे।
- चरण संख्या में। 5 यदि आप नोटिस करते हैं कि 7 3 से अधिक है, तो हम उनका आदान-प्रदान करेंगे और इसे अगले चरण में शामिल करेंगे और इसके विपरीत।
- अंत में, आप देखेंगे कि हमारी सरणी आरोही क्रम में क्रमबद्ध हो रही है।
मर्ज सॉर्ट के लिए प्रोग्राम
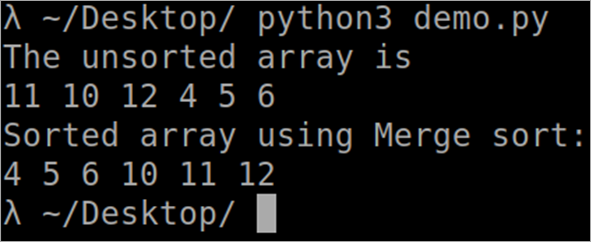
``` def MergeSort(arr): if len(arr) > 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i len(L) and j len(R): if L[i] R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i len(L): arr[k] = L[i] i += 1 k += 1 while j len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i in range(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Given array is", end="\n") PrintSortedList(arr) MergeSort(arr) print("Sorted array is: ", end="\n") PrintSortedList(arr) ```आउटपुट
मर्ज सॉर्ट की समय जटिलता
- सबसे खराब स्थिति: मर्ज सॉर्ट के लिए सबसे खराब समय जटिलता O( nहै 5> log( n )).
- औसत केस: मर्ज सॉर्ट के लिए औसत समय जटिलता O( n log(4) है>n )).
- सर्वश्रेष्ठ स्थिति: मर्ज सॉर्ट के लिए सर्वोत्तम समय जटिलता O( n हैlog( n )).
लाभ
- इस सॉर्टिंग तकनीक के लिए फ़ाइल का आकार मायने नहीं रखता।15
- यह तकनीक उन डेटा के लिए अच्छी है जो आम तौर पर अनुक्रम क्रम में एक्सेस किए जाते हैं। उदाहरण के लिए, लिंक की गई सूचियां, टेप ड्राइव आदि। सॉर्टिंग तकनीकें।
- यह दूसरों की तुलना में तुलनात्मक रूप से कम कुशल है।
त्वरित सॉर्ट
त्वरित सॉर्ट फिर से एक सूची के तत्वों को सॉर्ट करने के लिए विभाजित करें और जीतें विधि का उपयोग करता है। या एक सरणी। यह धुरी तत्वों को लक्षित करता है और चयनित धुरी तत्व के अनुसार तत्वों को क्रमबद्ध करता है। ,8,3,9,4,5,7 ”।
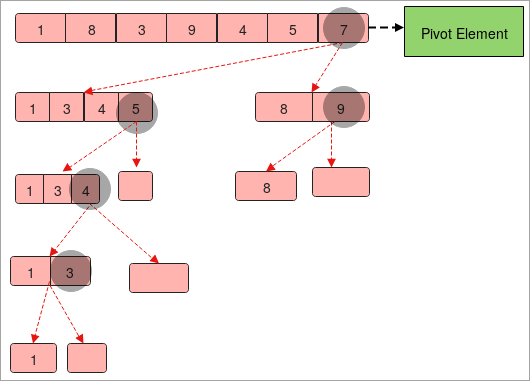
क्विक सॉर्ट के लिए प्रोग्राम
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] = pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i ] arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ] return ( i+1 ) def QuickSort( arr, lowest, highest ): if len( arr ) == 1: return arr if lowest highest: pi = Array_Partition( arr, lowest, highest ) QuickSort( arr, lowest, pi-1 ) QuickSort( arr, pi+1, highest ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Unsorted array: ", arr ) QuickSort( arr, 0, n-1 ) print( " Sorted array using Quick Sort: " ) for i in range( n ): print( " %d " % arr[ i ] ) ```
आउटपुट
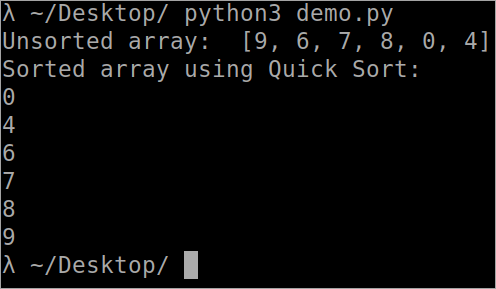
त्वरित सॉर्ट की समय जटिलता
- सबसे खराब स्थिति: त्वरित सॉर्ट के लिए सबसे खराब समय जटिलता O(4) है>n 2).
- औसत मामला: त्वरित छँटाई के लिए औसत समय जटिलता O( n log( n ) है .
- सर्वश्रेष्ठ मामला: त्वरित छँटाई के लिए सर्वोत्तम समय जटिलता O( n log( n )) है।
लाभ
- इसे पायथन में सर्वश्रेष्ठ छँटाई एल्गोरिथ्म के रूप में जाना जाता है।
- यह बड़ी मात्रा में डेटा को संभालने के दौरान उपयोगी है।15
- इसके लिए अतिरिक्त स्थान की आवश्यकता नहीं है।
नुकसान
- इसकी सबसे खराब स्थिति बबल सॉर्ट की जटिलताओं के समान है इंसर्शन सॉर्ट।
- जब हमारे पास पहले से ही सॉर्ट की गई सूची है तो यह सॉर्टिंग विधि उपयोगी नहीं है।
हीप सॉर्ट
हीप सॉर्ट बाइनरी सर्च ट्री का उन्नत संस्करण है . हीप सॉर्ट में, किसी सरणी का सबसे बड़ा तत्व हमेशा पेड़ की जड़ पर रखा जाता है, इसकी तुलना लीफ नोड्स के रूट से की जाती है।
उदाहरण के लिए:
- हमें "40, 100, 30, 50, 10" तत्वों वाली एक सरणी प्रदान की गई है।
- "चरण 1" में हमने इसके अनुसार एक पेड़ बनाया सरणी में तत्वों की उपस्थिति।

- “ चरण 2” में हम एक अधिकतम हीप बना रहे हैं यानी की व्यवस्था करने के लिए अवरोही क्रम में तत्व। सबसे बड़ा तत्व होगाशीर्ष (जड़) पर रहते हैं और सबसे छोटा तत्व नीचे (पत्ती नोड्स) पर रहता है। दी गई सरणी "100, 50, 30, 40, 10" बन जाती है।

- "चरण 3" में, हम न्यूनतम ढेर बना रहे हैं ताकि हम सरणी के न्यूनतम तत्वों को ढूंढ सकें। ऐसा करने से हमें अधिकतम और न्यूनतम तत्व मिलते हैं। हमें सॉर्ट किया गया ऐरे मिलता है।
हीप सॉर्ट की समय जटिलता
- सबसे खराब स्थिति: हीप सॉर्ट के लिए सबसे खराब समय जटिलता है O( n log( n )).
- औसत केस: हीप सॉर्ट के लिए औसत समय जटिलता O( n है log( n )).
- सबसे अच्छा मामला: हीप सॉर्ट के लिए सबसे अच्छा समय जटिलता हैO( n log(4)>n ))।
फायदे
- इसका उपयोग ज्यादातर इसकी उत्पादकता के कारण किया जाता है।
- यह कर सकता है इन-प्लेस एल्गोरिद्म के रूप में लागू किया जा सकता है।
- इसके लिए बड़े भंडारण की आवश्यकता नहीं है।
नुकसान
- इसके लिए स्थान की आवश्यकता है तत्वों को क्रमबद्ध करना।
- यह तत्वों को क्रमबद्ध करने के लिए पेड़ बनाता है।
छँटाई तकनीकों के बीच तुलना
छँटाई विधि सर्वश्रेष्ठ केस टाइम जटिलता औसत केस टाइम जटिलता सबसे खराब केस टाइम जटिलता स्पेस जटिलता स्थिरता इन -