Learje hoe't jo de Python Sort-funksje brûke foar it sortearjen fan listen, arrays, wurdboeken, ensfh mei ferskate sortearmetoaden en algoritmen yn Python:
Sortearjen is in technyk dy't brûkt wurdt foar it sortearjen de gegevens yn folchoarder of yn oprinnende of ôfnimmende folchoarder.
Meastentiids binne de gegevens fan de grutte projekten net yn de juste folchoarder regele en dat soarget foar problemen by it effisjint tagong en opheljen fan de nedige gegevens.
Sorteringstechniken wurde brûkt om dit probleem op te lossen. Python leveret ferskate sortearringstechniken bygelyks Bubble sort, Insertion sort, Merge sort, Quicksort, ensfh
Yn dizze tutorial sille wy begripe hoe't sortearjen yn Python wurket troch ferskate algoritmen te brûken.
Python Sort

Syntaksis fan Python Sort
Om it sortearjen út te fieren, leveret Python de ynboude funksje, d.w.s. de funksje " sort () ". It wurdt brûkt om de gegevens-eleminten fan in list yn oprinnende folchoarder of yn ôfnimmende folchoarder te sortearjen.
Litte wy dit konsept mei in foarbyld begripe.
Foarbyld 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( “ List in ascending order: ”, a ) ```
Utfier:

Yn dit foarbyld wurdt de opjûne net-oardere list yn oprinnende folchoarder sortearre troch de funksje " sort( ) " te brûken .
Foarbyld 2:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( “ List in descending order: ”, a ) ```
Utfier

Yn it boppesteande foarbyld, de opjûne net-oardere list wurdt yn omkearde folchoarder sortearre mei de funksje " sort( reverse = True ) ".
Tiidplak Bubble sortearje O(n) O(n2) O(n2) O(1) Ja Ja Sorte ynfoegje O(n) O(n2) 41>O(n2) 41>O(1) Ja Ja Snelle sortearje O(n log(n)) O(n log(n)) O(n2) O(N) Nee Ja Fúzje sort O(n log(n)) O(n log(n)) O(n log(n)) O(N) Ja Nee Heap sort O(n log (n)) O(n log(n)) O(n log(n)) O(1) Nee Ja
Yn de boppesteande fergelikingstabel "O" is de Big Oh notaasje hjirboppe útlein, wylst "n" en "N" de grutte fan 'e ynfier betsjutte .
Faak stelde fragen
F #1) Wat is sort () yn Python?
Antwurd: Yn Python sort() is in funksje dy't brûkt wurdt om de listen of arrays yn in spesifike folchoarder te sortearjen. Dizze funksje makket it sortearjen makliker by it wurkjen oan grutte projekten. It is tige nuttich foar de ûntwikkelders.
Q #2) Hoe sortearje jo yn Python?
Antwurd: Python leveret ferskate sorteartechniken dy't brûkt wurde om it elemint te sortearjen. Bygelyks, Fluch sortearje, Sortearje gearfoegje, Bubble sortearje, Sortearje ynfoegje, ensfh. Alle sorteartechniken binne effisjint en maklik te begripen.
Q #3) Hoe docht Python sortearje () wurk?
Antwurd: De sort()funksje nimt de opjûne array as in ynfier fan 'e brûker en sortearret it yn in spesifike folchoarder mei it sortearalgoritme. De seleksje fan it algoritme hinget ôf fan de kar fan de brûker. Brûkers kinne Quick sortearje, Merge sort, Bubble sort, Insertion sort, ensfh ôfhinklik fan de behoeften fan de brûker brûke.
Konklúzje
Yn it boppesteande tutorial hawwe wy de sorteartechnyk yn Python besprutsen tegearre mei de algemiene sortearring techniques.
- Bubble Sort
- Insertion Sort
- Quick Sort
Wy learden oer harren tiid kompleksiteit en foardielen & amp; neidielen. Wy fergelike ek alle boppesteande techniken.
Kompleksiteit fan sortearjen fan algoritmenTiid kompleksiteit is de hoemannichte tiid dy't de kompjûter nimt om in bepaald algoritme út te fieren. It hat trije soarten gefallen fan tiidkompleksiteit.
- Slimste gefal: Maksimum tiid dy't de kompjûter nimt om it programma út te fieren.
- Gemiddelde gefal: Tiid nommen tusken it minimum en maksimum troch de kompjûter om it programma út te fieren.
- Bêste gefal: Minimale tiid dy't de kompjûter nimt om it programma út te fieren. It is it bêste gefal fan tiidkompleksiteit.
Complexity Notations
Big Oh Notation, O: Big oh notaasje is de offisjele manier om de boppegrins oer te bringen fan rinnende tiid fan de algoritmen. It wurdt brûkt om de tiidskompleksiteit yn it slimste gefal te mjitten of wy sizze de grutste hoemannichte tiid dy't it algoritme nimt om te foltôgjen.
Big omega Notation,  : Big omega notation is de offisjele manier om de leechste grins fan 'e rinnende tiid fan' e algoritmen oer te bringen. It wurdt brûkt om best-case tiid kompleksiteit te mjitten of wy sizze de poerbêste hoemannichte tiid dy't it algoritme nimt.
: Big omega notation is de offisjele manier om de leechste grins fan 'e rinnende tiid fan' e algoritmen oer te bringen. It wurdt brûkt om best-case tiid kompleksiteit te mjitten of wy sizze de poerbêste hoemannichte tiid dy't it algoritme nimt.
Theta Notation, 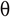 : Theta notation is the official way to convey beide grinzen i.e dy't de brute krêfttechnyk brûkt. It sil iterearje nei elk gegevenselemint en fergelykje it mei oare elemintenom de brûker de sortearre gegevens te jaan.
: Theta notation is the official way to convey beide grinzen i.e dy't de brute krêfttechnyk brûkt. It sil iterearje nei elk gegevenselemint en fergelykje it mei oare elemintenom de brûker de sortearre gegevens te jaan.
Lit ús in foarbyld nimme om dizze technyk te begripen:
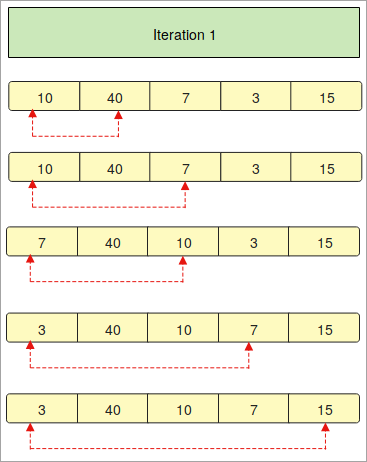
- Wy binne foarsjoen fan in array mei de eleminten " 10, 40, 7, 3, 15”. No moatte wy dizze array yn in oprinnende folchoarder regelje mei de Bubble-sorttechnyk yn Python.
- De alderearste stap is om de array yn de opjûne folchoarder te regeljen.
- Yn de " Iteraasje 1 " fergelykje wy it earste elemint fan in array ien foar ien mei de oare eleminten.
- De reade pylken beskriuwe de fergeliking fan de earste eleminten mei de oare eleminten fan in array.
- As jo merke dat " 10 " lytser is as " 40 ", dan bliuwt it itselde plak, mar it folgjende elemint " 7 " is lytser as " 10 ". Dêrtroch wurdt it ferfongen en komt it op it earste plak.
- It boppesteande proses sil hieltyd wer útfierd wurde om de eleminten te sortearjen.
-
- Yn de " Iteraasje 2 " wurdt it twadde elemint fergelike mei de oare eleminten fan in array.
- As it fergelike elemint lyts is dan sil it ferfongen wurde, oars bliuwt it op itselde plak.

-
- Yn " Iteraasje 3 " it tredde elemint wurdt fergelike mei de oare eleminten fan in array.

-
- Yn de lêste " Iteraasje 4 " it twadde lêste elemint wurdt fergelike mei de oare eleminten fan in array.
- Indizze stap wurdt de array yn oprinnende folchoarder sortearre.

Programma foar Bubble sortearje
``` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Unsorted List: ", unsorted_list) print("Sorted List using Bubble Sort Technique: ", Bubble_Sort(unsorted_list)) ``` Utfier

Tiidkompleksiteit fan bubbelsoarte
- Slimste gefal: De minste tiidkompleksiteit foar bubbelsoarte is O( n 2).
- Gemiddelde gefal: De gemiddelde tiidkompleksiteit foar bubbelsoarte is O( n 2).
- Bêste gefal: De bêste tiidkompleksiteit foar bubbelsoarte is O(n).
Foardielen
- It wurdt meast brûkt en is maklik te ymplementearjen.
- Wy kinne de gegevenseleminten wikselje sûnder konsumpsje fan koarte termyn opslach.
- It fereasket minder romte.
Neidielen
- It die net goed by it omgean mei in grut tal grutte data-eleminten.
- It hat n 2 stappen nedich foar elk "n" oantal gegevenseleminten om te sortearjen.
- It is net echt goed foar echte applikaasjes.
Ynfoegje Sortearje
Sortearje ynfoegje is in maklike en ienfâldige sorteartechnyk dy't fergelykber is mei it sortearjen fan de spylkaarten. Insertion sort sortearret de eleminten troch elk elemint ien foar ien te fergelykjen mei de oare. De eleminten wurde plukt en ferwiksele mei it oare elemint as it elemint grutter of lytser is as it oare.
Litte wy in foarbyld nimme
- Wy binne foarsjoen fan in array mei de eleminten " 100, 50, 30, 40, 10 ".
- Earst regelje wy de array en begjinne te fergelykjenit.
- Yn de earste stap wurdt " 100 " fergelike mei it twadde elemint " 50 ". " 50 " wurdt ferwiksele mei " 100 " om't it grutter is.
- Yn de twadde stap wurdt it twadde elemint " 100 " wer fergelike mei it tredde elemint " 30 " en wurdt wiksele.
- No, as jo merke dat " 30 " op it earste plak komt omdat it wer lytser is as " 50 ".
- De fergeliking sil foarkomme oant it lêste elemint fan in array en oan 'e ein krije wy de sortearre gegevens.

Programma foar ynfoegje sortearje
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j >= 0 and key_value array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("The unsorted array: ", array) InsertionSort(array) print ("The sorted array using the Insertion Sort: ") for i in range(len(array)): print (array[i]) ``` Utfier
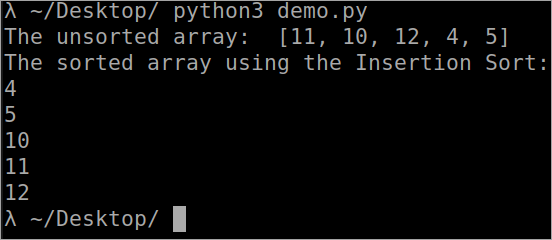
Tiid kompleksiteit fan ynfoegje sortearje
- Slimste gefal: De minste tiid kompleksiteit foar ynfoegje sort is O( n 2).
- Gemiddelde gefal: De gemiddelde tiidkompleksiteit foar Ynfoegje sortearje is O( n 2).
- Bêste gefal: De bêste tiidkompleksiteit foar Ynfoegje sortearje is O(n).
Foardielen
- It is ienfâldich en maklik te ymplementearjen.
- It docht goed by it omgean mei in lyts oantal gegevens-eleminten.
- It hat net mear romte nedich foar de ymplemintaasje.
Neidielen
- It is net nuttich om in grut tal data-eleminten te sortearjen.
- Yn ferliking mei oare sorteartechniken docht it net goed.
Sortearje gearfoegje
Dizze sortearmetoade brûkt de ferdieling en feroverje metoade om de eleminten yn in spesifike folchoarder te sortearjen. Wylst sortearjen mei help fan fusearje sort, deeleminten wurde ferdield yn helten en dan wurde se sortearre. Nei it sortearjen fan alle helten komme de eleminten wer byinoar om in perfekte folchoarder te foarmjen.
Litte wy in foarbyld nimme om dizze technyk te begripen
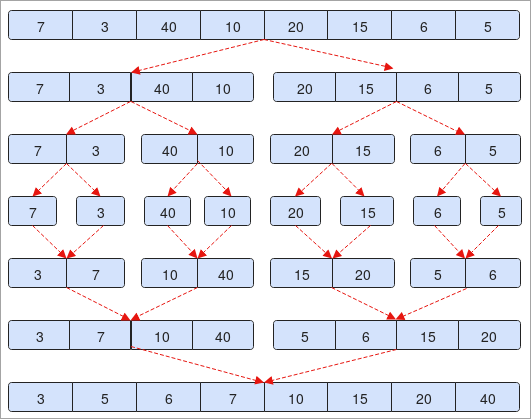
- Wy binne foarsjoen fan in rige "7, 3, 40, 10, 20, 15, 6, 5". De array befettet 7 eleminten. As wy it yn de helte diele ( 0 + 7 / 2 = 3 ).
- Yn de twadde stap sille jo sjen dat de eleminten yn twa dielen ferdield binne. Elk hat 4 eleminten deryn.
- Fierder wurde de eleminten wer ferdield en hawwe elk 2 eleminten.
- Dit proses sil trochgean oant mar ien elemint oanwêzich is yn in array. Ferwize nei stap nr. 4 op de foto.
- No sille wy de eleminten sortearje en begjinne mei te ferbinen sa't wy ferdield binne.
- Yn stap nr. 5 as jo merke dat 7 grutter is dan 3, dus wy sille se wikselje en meidwaan yn 'e folgjende stap en oarsom.
- Oan 'e ein sille jo merke dat ús array yn oprinnende folchoarder wurdt sortearre.
Programma foar sortearje gearfoegje
``` def MergeSort(arr): if len(arr) > 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i len(L) and j len(R): if L[i] R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i len(L): arr[k] = L[i] i += 1 k += 1 while j len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i in range(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Given array is", end="\n") PrintSortedList(arr) MergeSort(arr) print("Sorted array is: ", end="\n") PrintSortedList(arr) ``` Utfier
Tiidkompleksiteit fan sortearje gearfoegje
- Slimste gefal: De minste tiidkompleksiteit foar sortearring gearfoegje is O( n log( n )).
- Gemiddelde gefal: De gemiddelde tiidkompleksiteit foar fusearje is O( n log( >n )).
- Bêste gefal: De bêste tiidkompleksiteit foar fusearje is O( n log( n )).
Foardielen
- De triemgrutte makket net út foar dizze sorteartechnyk.
- Dizze technyk is goed foar de gegevens dy't oer it algemien tagonklik binne yn in folchoarder. Bygelyks keppele listen, tapedrive, ensfh.
Neidielen
- It freget mear romte yn ferliking mei oare sortearringstechniken.
- It is fergelykber minder effisjint as oaren.
Fluch sortearje
Fluch sortearje brûkt wer de ferdieling en feroverje metoade om de eleminten fan in List te sortearjen of in array. It rjochtet de pivot-eleminten en sortearret de eleminten neffens it selektearre pivot-elemint.
Bygelyks
- Wy binne foarsjoen fan in array mei de eleminten " 1 ,8,3,9,4,5,7 ”.
- Lit ús oannimme dat “7” in pilotelemint is.
- No sille wy de array op sa'n manier diele dat de lofterkant befettet de eleminten dy't lytser binne as it pivot elemint " 7 " en de rjochterkant befettet de eleminten grutter dan it pivot elemint " 7 ".
- Wy hawwe no twa arrays " 1,3,4,5 ” en “ 8, 9 ”.
- Wer moatte wy beide arrays krekt sa ferdield as hjirboppe. It ienige ferskil is dat de pivot-eleminten wizige wurde.
- Wy moatte de arrays diele oant wy it inkelde elemint yn 'e array krije.
- Sammelje oan 'e ein alle pivot-eleminten yn in folchoarder fan links nei rjochts en jo krije it sortearrearray.
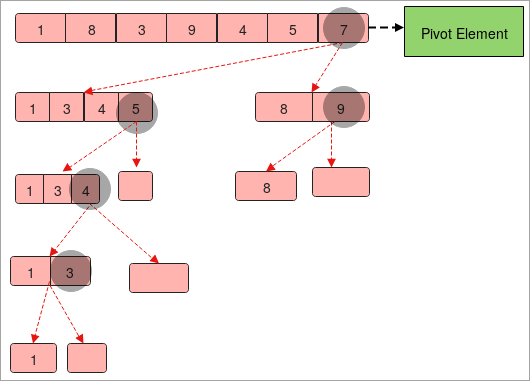
Programma foar fluch sortearje
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] = pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i ] arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ] return ( i+1 ) def QuickSort( arr, lowest, highest ): if len( arr ) == 1: return arr if lowest highest: pi = Array_Partition( arr, lowest, highest ) QuickSort( arr, lowest, pi-1 ) QuickSort( arr, pi+1, highest ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Unsorted array: ", arr ) QuickSort( arr, 0, n-1 ) print( " Sorted array using Quick Sort: " ) for i in range( n ): print( " %d " % arr[ i ] ) ```
Utfier
Tiidkompleksiteit fan Quick sortearje
- Slimste gefal: De minste tiidkompleksiteit foar Quick sortearje is O( n 2).
- Gemiddelde gefal: De gemiddelde tiidkompleksiteit foar Quick sortearje is O( n log( n ) ).
- Bêste gefal: De bêste tiidkompleksiteit foar Quick sortearje is O( n log( n )).
Foardielen
- It stiet bekend as it bêste sortearalgoritme yn Python.
- It is nuttich by it behanneljen fan in grutte hoemannichte gegevens.
- It hat gjin ekstra romte nedich.
Neidielen
- De kompleksiteit fan it slimste gefal is fergelykber mei de kompleksiteiten fan bubbelsoarte en ynfoegje sort.
- Dizze sortearring metoade is net brûkber as wy al hawwe de sortearre list.
Heap sort
Heap sort is de avansearre ferzje fan Binary search tree . Yn heapsoarte wurdt it grutste elemint fan in rige altyd en dan op 'e woartel fan 'e beam pleatst, fergelike mei de woartel mei de blêdknoppen.
Bygelyks:
- Wy binne foarsjoen fan in array mei de eleminten " 40, 100, 30, 50, 10 ".
- Yn " stap 1 " hawwe wy in beam makke neffens de oanwêzigens fan de eleminten yn de array.

- Yn “ stap 2 ” meitsje wy in maksimale heap d.w.s. eleminten yn de delgeande folchoarder. It grutste elemint silwenje oan 'e boppekant (root) en it lytste elemint wennet oan' e ûnderkant (blêdknoppen). De opjûne array wurdt "100, 50, 30, 40, 10".

- Yn " stap 3 " , wy meitsje de minimale heap sadat wy de minimale eleminten fan in array kinne fine. Troch dit te dwaan krije wy de maksimum en de minimale eleminten.

- Yn “ stap 4 ” troch deselde stappen út te fieren wy krije de sortearre array.

Programma foar Heap sortearje
``` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left n and arr[ larger_element ] arr[ left ]: larger_element = left if right n and arr[ larger_element ] arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ] HeapSortify( arr, n, larger_element ) def HeapSort( arr ): n = len( arr ) for i in range( n//2 - 1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " The unsorted array is: ", arr ) HeapSort( arr ) n = len( arr ) print( " The sorted array sorted by the Heap Sort: " ) for i in range( n ): print( arr[ i ] ) ```
Utfier
Tiidkompleksiteit fan Heap-soarte
- Slimste gefal: De minste tiidkompleksiteit foar Heap-soarte is O( n log( n )).
- Gemiddelde gefal: De gemiddelde tiidkompleksiteit foar Heap sort is O( n log( n )).
- Bêste gefal: De bêste tiidkompleksiteit foar Heap sort isO( n log( >n )).
Foardielen
- It wurdt meast brûkt fanwegen syn produktiviteit.
- It kin wurde ymplemintearre as in algoritme op it plak.
- It hat gjin grutte opslach nedich.
Nearmen
- Need romte foar sortearjen fan de eleminten.
- It makket de beam foar it sortearjen fan de eleminten.
Fergeliking tusken de sorteartechniken
| Sorteringsmetoade | Bêste gefal tiid kompleksiteit | Gemiddelde gefal tiid kompleksiteit | Slimste gefal tiid kompleksiteit | Romte kompleksiteit | Stabiliteit | In - |
|---|