Навучыцеся выкарыстоўваць функцыю сартавання Python для сартавання спісаў, масіваў, слоўнікаў і г.д. з выкарыстаннем розных метадаў і алгарытмаў сартавання ў Python:
Сартаванне - гэта метад, які выкарыстоўваецца для сартавання дадзеныя ў парадку паслядоўнасці альбо ў парадку ўзрастання, альбо ў парадку змяншэння.
Часцей за ўсё даныя буйных праектаў размешчаны не ў правільным парадку, і гэта стварае праблемы пры эфектыўным доступе да неабходных даных і іх атрыманні.
Для вырашэння гэтай праблемы выкарыстоўваюцца метады сартавання. Python забяспечвае розныя метады сартавання напрыклад, сартаванне бурбалкамі, сартаванне ўстаўкай, сартаванне зліццём, хуткае сартаванне і г.д.
У гэтым уроку мы зразумеем, як працуе сартаванне ў Python з выкарыстаннем розных алгарытмаў.
Сартаванне Python

Сінтаксіс сартавання Python
Для выканання сартавання Python забяспечвае ўбудаваную функцыю, напрыклад функцыю «sort()». Ён выкарыстоўваецца для сартавання элементаў дадзеных спісу ў парадку ўзрастання або змяншэння.
Давайце разбярэмся ў гэтай канцэпцыі на прыкладзе.
Прыклад 1:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort() print( “ List in ascending order: ”, a ) ```
Вывад:

У гэтым прыкладзе дадзены неўпарадкаваны спіс адсартаваны ў парадку ўзрастання з дапамогай функцыі « sort( ) » .
Прыклад 2:
``` a = [ 3, 5, 2, 6, 7, 9, 8, 1, 4 ] a.sort( reverse = True ) print( “ List in descending order: ”, a ) ```
Вывад

У прыведзеным вышэй прыкладзе, дадзены неўпарадкаваны спіс сартуецца ў адваротным парадку з дапамогай функцыі “ sort( reverse = True ) ”.
Часмесца Сартаванне бурбалкамі O(n) O(n2) O(n2) O(1) Так Так Сартаванне ўстаўкай O(n) O(n2) O(n2) O(1) Так Так Хуткае сартаванне O(n log(n)) O(n log(n)) O(n2) O(N) Не Так Аб'яднаць сартаваць O(n log(n)) O(n log(n)) O(n log(n)) O(N) Так Не Сартаванне кучы O(n журнал (n)) O(n log(n)) O(n log(n)) O(1) Не Так
У прыведзенай вышэй параўнальнай табліцы « O » - гэта абазначэнне Big Oh, якое тлумачылася вышэй, тады як « n » і « N » азначаюць памер уводу .
Часта задаюць пытанні
Пытанне №1) Што такое sort () у Python?
Адказ: У Python sort() - гэта функцыя, якая выкарыстоўваецца для сартавання спісаў або масіваў у пэўным парадку. Гэтая функцыя палягчае працэс сартавання пры працы над вялікімі праектамі. Гэта вельмі карысна для распрацоўшчыкаў.
Q #2) Як вы сартуеце ў Python?
Адказ: Python забяспечвае розныя метады сартавання, якія выкарыстоўваюцца для сартавання элемента. Напрыклад, Хуткае сартаванне, сартаванне зліццём, сартаванне па тыпу бурбалкі, сартаванне па ўстаўцы і г.д. Усе метады сартавання эфектыўныя і простыя для разумення.
Q #3) Як працуе Python сартаваць () працаваць?
Адказ: Сартаванне()Функцыя прымае зададзены масіў як увод ад карыстальніка і сартуе яго ў пэўным парадку з дапамогай алгарытму сартавання. Выбар алгарытму залежыць ад выбару карыстальніка. Карыстальнікі могуць выкарыстоўваць хуткае сартаванне, сартаванне аб'яднаннем, сартаванне па тыпу бурбалкі, сартаванне ўстаўкай і г.д. у залежнасці ад патрэбаў карыстальніка.
Выснова
У прыведзеным вышэй падручніку мы абмяркоўвалі тэхніку сартавання ў Python разам з агульныя метады сартавання.
- Сартаванне бурбалкамі
- Сартаванне ўстаўкай
- Хуткае сартаванне
Мы даведаліся аб іх часавых складанасці і перавагах & недахопы. Мы таксама параўналі ўсе вышэйпералічаныя метады.
Складанасць алгарытмаў сартаванняЧасовая складанасць - гэта колькасць часу, якое патрабуецца камп'ютару для запуску пэўнага алгарытму. Ён мае тры тыпы складанасці па часе.
- Горшы выпадак: Максімальны час, неабходны камп'ютару для выканання праграмы.
- Сярэдні выпадак: Час, неабходны камп'ютару для выканання праграмы паміж мінімальным і максімальным.
- Найлепшы выпадак: Мінімальны час, неабходны камп'ютару для запуску праграмы. Гэта лепшы выпадак часавай складанасці.
Абазначэнні складанасці
Вялікае абазначэнне О, O: Абазначэнне Вялікае о з'яўляецца афіцыйным спосабам перадачы верхняй мяжы час працы алгарытмаў. Ён выкарыстоўваецца для вымярэння складанасці часу ў найгоршым выпадку, або мы кажам, што найбольшы час, неабходны алгарытму для выканання.
Вялікая амега-абазначэнне,  : Вялікая амега-абазначэнне афіцыйны спосаб перадаць найменшую мяжу часу працы алгарытмаў. Ён выкарыстоўваецца для вымярэння аптымальнай часавай складанасці або, як мы кажам, выдатнай колькасці часу, затрачанага алгарытмам.
: Вялікая амега-абазначэнне афіцыйны спосаб перадаць найменшую мяжу часу працы алгарытмаў. Ён выкарыстоўваецца для вымярэння аптымальнай часавай складанасці або, як мы кажам, выдатнай колькасці часу, затрачанага алгарытмам.
Тэта-абазначэнне, 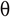 : Тэта-абазначэнне з'яўляецца афіцыйным спосабам перадачы абедзве межы, г.зн. ніжняя і верхняя часткі часу, неабходнага алгарытму для выканання.
: Тэта-абазначэнне з'яўляецца афіцыйным спосабам перадачы абедзве межы, г.зн. ніжняя і верхняя часткі часу, неабходнага алгарытму для выканання.
Метады сартавання ў Python
Сартаванне па тыпу бурбалкі
Сартаванне па тыпу бурбалкі - гэта самы просты спосаб сартавання даных які выкарыстоўвае тэхніку грубай сілы. Ён будзе паўтараць кожны элемент дадзеных і параўноўваць яго з іншымі элементамікаб даць карыстальніку адсартаваныя даныя.
Давайце возьмем прыклад, каб зразумець гэтую тэхніку:
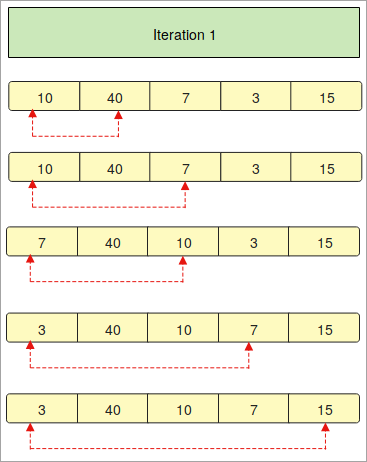
- Нам прадастаўляецца масіў з элементамі « 10, 40, 7, 3, 15”. Цяпер нам трэба арганізаваць гэты масіў у парадку ўзрастання, выкарыстоўваючы тэхніку Bubble сартавання ў Python.
- Самым першым крокам з'яўляецца размяшчэнне масіва ў зададзеным парадку.
- У «Ітэрацыі 1» мы параўноўваем першы элемент масіва з іншымі элементамі адзін за адным.
- Чырвоныя стрэлкі апісваюць параўнанне першых элементаў з іншымі элементамі масіва.
- Калі вы заўважылі, што « 10 » меншае за « 40 », значыць, яно застаецца ранейшым месца, але наступны элемент «7» меншы за «10». Такім чынам, ён замяняецца і выходзіць на першае месца.
- Апісаны вышэй працэс будзе выконвацца зноў і зноў для сартавання элементаў.
-
- У « Ітэрацыі 2 » другі элемент параўноўваецца з іншымі элементамі масіва.
- Калі параўноўваны элемент малы, ён будзе быць заменены, у адваротным выпадку ён застанецца на тым самым месцы.

-
- У « Ітэрацыя 3 » трэці элемент параўноўваецца з іншымі элементамі масіва.

-
- У апошнім « Ітэрацыя 4 » перадапошні элемент параўноўваецца з іншымі элементамі масіва.
- Уна гэтым этапе масіў сартуецца ў парадку ўзрастання.

Праграма для Bubble sort
``` def Bubble_Sort(unsorted_list): for i in range(0,len(unsorted_list)-1): for j in range(len(unsorted_list)-1): if(unsorted_list[j]>unsorted_list[j+1]): temp_storage = unsorted_list[j] unsorted_list[j] = unsorted_list[j+1] unsorted_list[j+1] = temp_storage return unsorted_list unsorted_list = [5, 3, 8, 6, 7, 2] print("Unsorted List: ", unsorted_list) print("Sorted List using Bubble Sort Technique: ", Bubble_Sort(unsorted_list)) ``` Вынік

Часовая складанасць бурбалкавага сартавання
- Найгоршы выпадак: Найгоршая часовая складанасць для бурбалкавага сартавання - O( n 2).
- Сярэдні выпадак: Сярэдняя часовая складанасць для бурбалкавага сартавання - O( n 2).
- Лепшы выпадак: Найлепшая часовая складанасць для бурбалкавага сартавання - O(n).
Перавагі
- Ён у асноўным выкарыстоўваецца і просты ў рэалізацыі.
- Мы можам замяняць элементы даных без выкарыстання кароткачасовага захоўвання.
- Гэта патрабуе менш прастора.
Недахопы
- Ён дрэнна працаваў пры працы з вялікай колькасцю вялікіх элементаў даных.
- Гэта патрабуецца n 2 крокі для кожнай «n» колькасці элементаў даных для сартавання.
- Гэта не вельмі добра для рэальных прыкладанняў.
Устаўка Сартаванне
Сартаванне ўстаўкай - гэта лёгкі і просты метад сартавання, які працуе падобна на сартаванне ігральных карт. Сартаванне ўстаўкай сартуе элементы, параўноўваючы кожны элемент адзін за адным. Элементы выбіраюцца і мяняюцца месцамі з іншымі элементамі, калі гэты элемент большы або меншы за другі.
Давайце возьмем прыклад
- Нам прадастаўляецца масіў з элементамі “ 100, 50, 30, 40, 10 ”.
- Спачатку мы ўпарадкоўваем масіў і пачынаем параўноўвацьit.
- На першым этапе “ 100 ” параўноўваецца з другім элементам “ 50 ”. “ 50 ” мяняецца месцамі на “ 100 ”, паколькі яно большае.
- На другім этапе зноў другі элемент “ 100 ” параўноўваецца з трэцім элементам “ 30 ” і мяняецца месцамі.
- Цяпер, калі вы заўважылі, што “ 30 ” стаіць на першым месцы, таму што яно зноў жа меншае за “ 50 ”.
- Параўнанне будзе адбывацца да апошняга элемента масіва, і ў канцы мы атрымаем адсартаваныя дадзеныя.

Праграма для сартавання ўстаўкі
``` def InsertionSort(array): for i in range(1, len(array)): key_value = array[i] j = i-1 while j >= 0 and key_value array[j] : array[j + 1] = array[j] j -= 1 array[j + 1] = key_value array = [11, 10, 12, 4, 5] print("The unsorted array: ", array) InsertionSort(array) print ("The sorted array using the Insertion Sort: ") for i in range(len(array)): print (array[i]) ``` Вывад
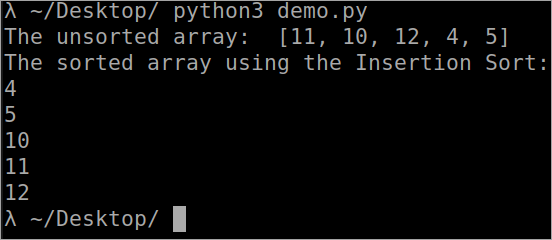
Часовая складанасць сартавання па ўстаўцы
- Найгоршы выпадак: Найгоршая па часе складанасць сартавання па ўстаўцы складае O( n 2).
- Сярэдні выпадак: Сярэдняя складанасць часу для сартавання ўстаўкай складае O( n 2).
- Найлепшы выпадак: Найлепшы час для сартавання ўстаўкай — O(n).
Перавагі
- Гэта проста і просты ў рэалізацыі.
- Ён добра працуе пры працы з невялікай колькасцю элементаў даных.
- Для яго рэалізацыі не патрабуецца больш месца.
Недахопы
- Не дапамагае сартаваць велізарную колькасць элементаў даных.
- У параўнанні з іншымі метадамі сартавання ён не працуе добра.
Сартаванне зліццём
Гэты метад сартавання выкарыстоўвае метад падзяляй і ўладар для сартавання элементаў у пэўным парадку. Падчас сартавання з дапамогай сартавання зліццём, theэлементы дзеляцца на палоўкі, а потым сартуюцца. Пасля сартавання ўсіх палоў элементы зноў злучаюцца ў ідэальны парадак.
Давайце возьмем прыклад, каб зразумець гэтую тэхніку
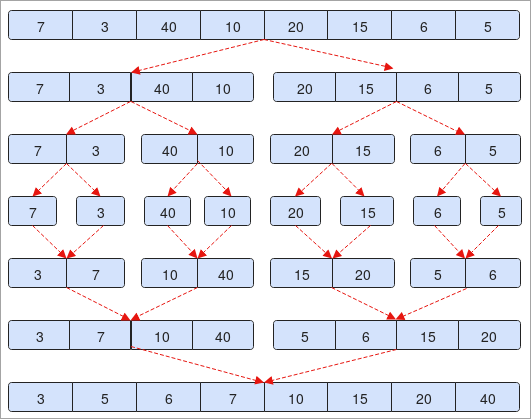
- У нас ёсць масіў «7, 3, 40, 10, 20, 15, 6, 5». Масіў змяшчае 7 элементаў. Калі мы падзелім яго напалову ( 0 + 7 / 2 = 3 ).
- На другім этапе вы ўбачыце, што элементы падзелены на дзве часткі. У кожным з іх па 4 элемента.
- Далей элементы зноў падзяляюцца і маюць па 2 элементы кожны.
- Гэты працэс будзе працягвацца, пакуль у масіве не будзе толькі аднаго элемента. Звярніцеся да кроку № 4 на малюнку.
- Цяпер мы адсартуем элементы і пачнем злучаць іх так, як мы былі падзелены.
- На этапе №. 5, калі вы заўважылі, што 7 больш за 3, таму мы абмяняем іх і аб'яднаем на наступным этапе, і наадварот.
- У канцы вы заўважыце, што наш масіў сартуецца ў парадку ўзрастання.
Праграма для сартавання зліццём
``` def MergeSort(arr): if len(arr) > 1: middle = len(arr)//2 L = arr[:middle] R = arr[middle:] MergeSort(L) MergeSort(R) i = j = k = 0 while i len(L) and j len(R): if L[i] R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 while i len(L): arr[k] = L[i] i += 1 k += 1 while j len(R): arr[k] = R[j] j += 1 k += 1 def PrintSortedList(arr): for i in range(len(arr)): print(arr[i],) print() arr = [12, 11, 13, 5, 6, 7] print("Given array is", end="\n") PrintSortedList(arr) MergeSort(arr) print("Sorted array is: ", end="\n") PrintSortedList(arr) ``` Вывад
Часовая складанасць сартавання зліццём
- Найгоршы выпадак: Найгоршы час сартавання зліццём складае O( n log( n )).
- Сярэдні выпадак: Сярэдняя складанасць часу для сартавання зліццём складае O( n log( n )).
- Найлепшы выпадак: Найлепшы час для сартавання зліццём складае O( n log( n )).
Перавагі
- Памер файла не мае значэння для гэтай методыкі сартавання.
- Гэты метад добры для даных, доступ да якіх звычайна ажыццяўляецца ў паслядоўным парадку. Напрыклад, звязаныя спісы, магнітафон і г.д.
Недахопы
- Ён патрабуе больш месца ў параўнанні з іншымі метады сартавання.
- Ён параўнальна менш эфектыўны, чым іншыя.
Хуткае сартаванне
Хуткае сартаванне зноў выкарыстоўвае метад падзяляй і ўладар для сартавання элементаў спісу або масіў. Ён арыентуецца на зводныя элементы і сартуе элементы ў адпаведнасці з абраным зводным элементам.
Напрыклад
- Нам прадастаўляецца масіў з элементамі “ 1 ,8,3,9,4,5,7 ”.
- Дапусцім, што “ 7 ” з'яўляецца пілотным элементам.
- Цяпер мы падзелім масіў такім чынам, каб левы бок змяшчае элементы, якія меншыя за асноўны элемент « 7 », а правы бок змяшчае элементы, большыя за асноўны элемент « 7 ».
- Цяпер у нас ёсць два масівы « 1,3,4,5 ” і “ 8, 9 ”.
- Зноў жа, мы павінны падзяліць абодва масівы гэтак жа, як мы рабілі вышэй. Адзіная розніца ў тым, што зводныя элементы змяняюцца.
- Нам трэба падзяліць масівы, пакуль не атрымаецца адзіны элемент у масіве.
- У канцы збярыце ўсе зводныя элементы ў паслядоўнасць злева направа, і вы атрымаеце адсартаваныямасіў.
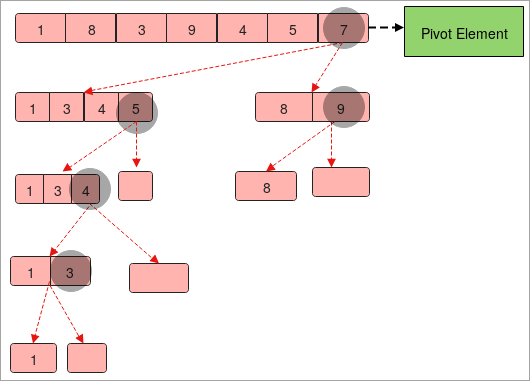
Праграма хуткага сартавання
``` def Array_Partition( arr, lowest, highest ): i = ( lowest-1 ) pivot_element = arr[ highest ] for j in range( lowest, highest ): if arr[ j ] = pivot_element: i = i+1 arr[ i ], arr[ j ] = arr[ j ], arr[ i ] arr[ i+1 ], arr[ highest ] = arr[ highest ], arr[ i+1 ] return ( i+1 ) def QuickSort( arr, lowest, highest ): if len( arr ) == 1: return arr if lowest highest: pi = Array_Partition( arr, lowest, highest ) QuickSort( arr, lowest, pi-1 ) QuickSort( arr, pi+1, highest ) arr = [ 9, 6, 7, 8, 0, 4 ] n = len( arr ) print( " Unsorted array: ", arr ) QuickSort( arr, 0, n-1 ) print( " Sorted array using Quick Sort: " ) for i in range( n ): print( " %d " % arr[ i ] ) ```
Вывад
Часовая складанасць хуткага сартавання
- Найгоршы выпадак: Найгоршы час для хуткага сартавання складае O( n 2).
- Сярэдні выпадак: Сярэдняя складанасць часу для хуткага сартавання складае O( n log( n ) ).
- Лепшы выпадак: Найлепшая часовая складанасць для хуткага сартавання - O( n log( n )).
Перавагі
- Ён вядомы як лепшы алгарытм сартавання ў Python.
- Ён карысны пры працы з вялікім аб'ёмам даных.
- Ён не патрабуе дадатковага месца.
Недахопы
- Яго складанасць у горшым выпадку падобная да складанасці сартавання бурбалкамі і сартаванне ўстаўкай.
- Гэты метад сартавання не карысны, калі ў нас ужо ёсць адсартаваны спіс.
Сартаванне кучы
Сартаванне кучы - гэта пашыраная версія двайковага дрэва пошуку . Пры сартаванні кучы найбольшы элемент масіва заўсёды размяшчаецца ў корані дрэва, а потым параўноўваецца з коранем з ліставымі вузламі.
Напрыклад:
- Нам прапанаваны масіў з элементамі “ 40, 100, 30, 50, 10 ”.
- На “кроку 1” мы стварылі дрэва ў адпаведнасці з наяўнасць элементаў у масіве.

- На “ крок 2 ” мы робім максімальную кучу, г.зн. элементы ў парадку змяншэння. Найвялікшы элемент будзезнаходзяцца ўверсе (корань), а найменшы элемент знаходзіцца ўнізе (ліставыя вузлы). Дадзены масіў становіцца “ 100, 50, 30, 40, 10 ”.

- На “кроку 3” мы ствараем мінімальную кучу, каб мы маглі знайсці мінімальныя элементы масіва. Робячы гэта, мы атрымліваем максімум і мінімум элементаў.

- На «кроку 4» выконваючы тыя ж дзеянні мы атрымліваем адсартаваны масіў.

Праграма для сартавання кучы
``` def HeapSortify( arr, n, i ): larger_element = i left = 2 * i + 1 right = 2 * i + 2 if left n and arr[ larger_element ] arr[ left ]: larger_element = left if right n and arr[ larger_element ] arr[ right ]: larger_element = right if larger_element != i: arr[ i ], arr[ larger_element ] = arr[ larger_element ], arr[ i ] HeapSortify( arr, n, larger_element ) def HeapSort( arr ): n = len( arr ) for i in range( n//2 - 1, -1, -1 ): HeapSortify( arr, n, i ) for i in range( n-1, 0, -1 ): arr[ i ], arr[ 0 ] = arr[ 0 ], arr[ i ] HeapSortify( arr, i, 0 ) arr = [ 11, 10, 12, 4, 5, 6 ] print( " The unsorted array is: ", arr ) HeapSort( arr ) n = len( arr ) print( " The sorted array sorted by the Heap Sort: " ) for i in range( n ): print( arr[ i ] ) ```
Вывад
Часовая складанасць сартавання кучы
- Найгоршы выпадак: Найгоршая часовая складанасць сартавання кучы: O( n log( n )).
- Сярэдні выпадак: Сярэдняя складанасць часу для сартавання кучы складае O( n log( n )).
- Найлепшы выпадак: Найлепшая часовая складанасць для сартавання кучы роўная O( n log( n )).
Перавагі
- Яно ў асноўным выкарыстоўваецца з-за сваёй прадукцыйнасці.
- Ён можа быць рэалізаваны як алгарытм на месцы.
- Ён не патрабуе вялікага сховішча.
Недахопы
- Неабходна месца для сартаванне элементаў.
- Гэта стварае дрэва для сартавання элементаў.
Параўнанне паміж метадамі сартавання
| Метад сартавання | Складанасць у найлепшым выпадку па часе | Сярэдняя складанасць па часе ў выпадку | Складанасць па часе ў найгоршым выпадку | Прасторавая складанасць | Стабільнасць | In - |
|---|